有一百份面包要分给5个人,第二个人比第一个人多分的量,等于第三个人比第二个人多分的量,也等于第四个人比第三个人多分的量,还等于第五个人比第四个人多分的量,另外,前面两个人分的

【题目】级数是一个古老的问题。在2000多年以前，国际象棋的发明者提出了报酬的问题，而这还不是最古老的。在埃及著名的林德氏草纸本中，有一个关于分面包的问题，要古老得多。这个草纸本是由林德氏在18世纪末发现的，据考证，它出现在公元前2000年左右。其中还提到了一些其他的数学著作，可能要追溯到公元前3000年左右。在这个草纸本中，有很多关于算术或者代数的题目。其中有一道是这样的：

有一百份面包要分给5个人。第二个人比第一个人多分的量，等于第三个人比第二个人多分的量，也等于第四个人比第三个人多分的量，还等于第五个人比第四个人多分的量。另外，前面两个人分的量是后面三个人分的量的¹₇。那么，每个人分得的面包是多少份？

【解答】很明显，每个人分得的面包数成递增的级数。假设第一个人分得的面包为x份，第二个人比第一个人多分了y份，则

第一个人的面包数…………………………x；

第二个人的面包数…………………………x+y；

第三个人的面包数…………………………x+2y；

第四个人的面包数…………………………x+3y；

第五个人的面包数…………………………x+4y。

根据题意，可以得到下面的方程组

第一个方程化简可得

x+2y=20

第二个方程化简可得

11x=2y

容易解得

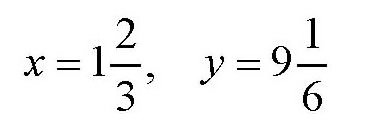
也就是说，这100份面包应该分成下面的5份