【题目】如图所示,在点A和点B之间,有一条两岸平行的运河。现在,想在这条运河上建造一座垂直于岸边的桥,那么应该选择什么位置,才能保证从点A到点B的距离最短?
【解答】如图所示,过点A作一条垂直于河流方向的直线,在直线上选取一点C,使AC等于河面的宽度,连接点B和点C,得到点D,在点D建造这座桥,就能保证点A和点B之间的距离最短。
如图所示,为什么将桥建在DE处,点A与点B之间的距离最短?下面我们就来证明一下。连接点E和点A,则线段AC平行且等于线段ED,四边形AEDC是平行四边形,AE平行于CD。因此,路径AEDB的长度等于ACB的长度。其实,可以很容易证明,任何一条别的路径都要比这条路经长。
如图所示,假设有一条路径AMNB比路径AEDB短,即比路径ACB短。连接点C和点N,得到:CN=AM,AMNB=ACNB,但是,路径CNB比路径CB长,所以,路径ACNB比路径ACB长,即路径ACNB比路径AEDB长。也就是说,刚才的假设是错误的,路径AMNB要比路径AEDB长。
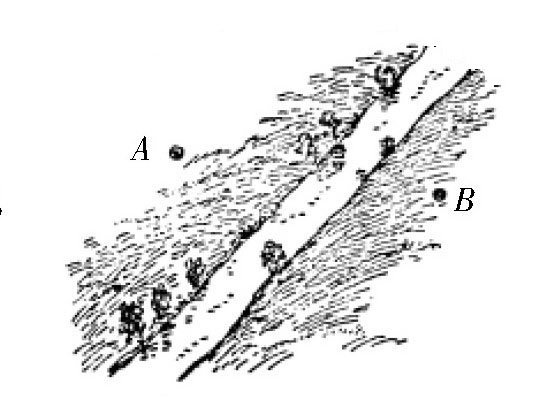
图 在哪里架桥,能使桥和岸边垂直,且从A点到B点路程最近?
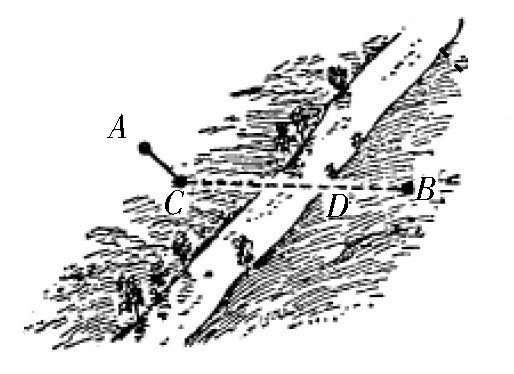
图 架桥位置示意图。
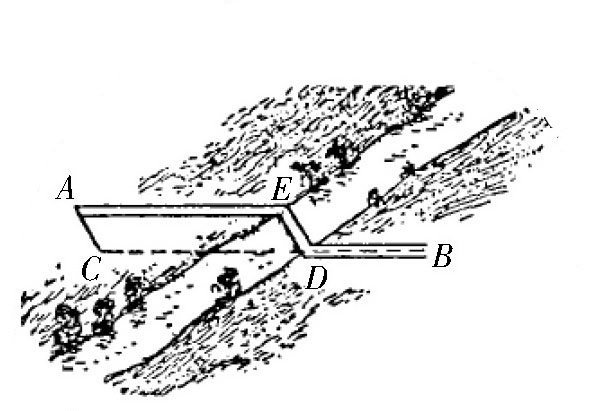
图 距离最短的桥。
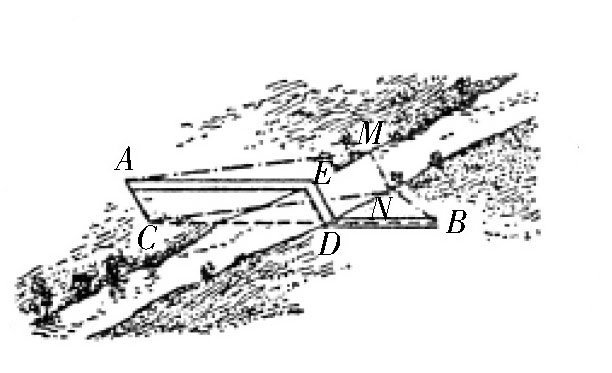
图 最短距离的桥的证明图示。
根据前面的分析,我们可以得出,如果换一个地方建造这座桥,根本不能保证距离最短,点D是唯一可以保证距离最短的地方。
