【题目】如图所示,要用圆形铁片做一个漏斗,需要切掉一个扇形。那么,切去的这个扇形内角应该为多少度,才能使做成漏斗的容量最大?

【解答】设切掉的扇形圆铁片弧长为x,半径为R。则做成的圆锥形漏斗的母线也是R,漏斗的底面周长为x。从而漏斗的底面半径r为:

根据勾股定理,圆锥的高为
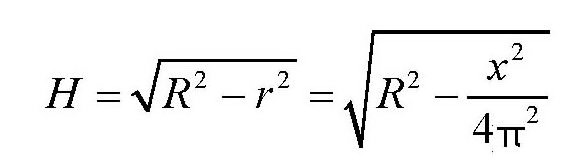
所以,圆锥的体积为
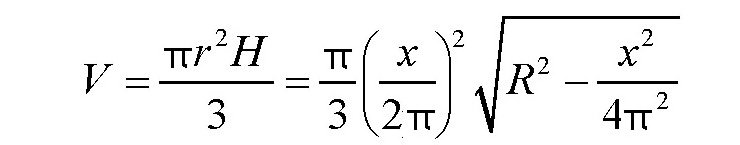
等式两边平方,并除以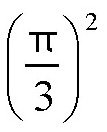
,再乘以2得
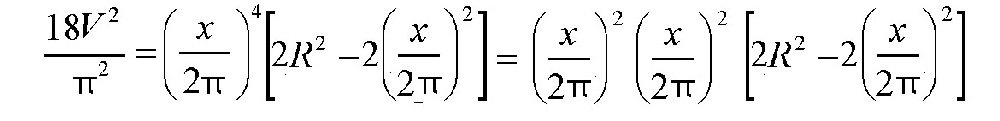
上式右边的3个乘数满足下面的关系:

这是一个定值。根据前面的结论,当
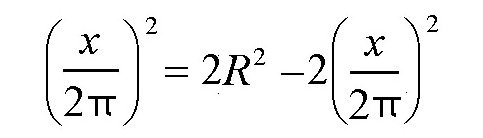
时,上面的式子取得最大值。此时
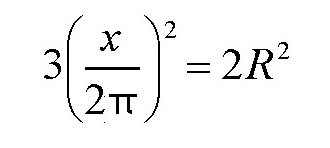
容易得出
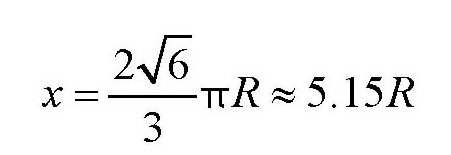
如果换算成弧度,大约是295°,即切掉的扇形内角应该为
360°-295°=65°
