【题目】一只雪橇从坡度为30°、长度为12米的滑道滑下来,然后沿着水平面继续向前滑行。请问,这只雪橇能滑多远?
【解答】如果忽略不计雪橇跟雪面之间的摩擦力,那么这只雪橇将会一直滑行下去,永远也不会停下来。但是,它们之间是有摩擦力的,虽然摩擦力是很小的。(通常来说,雪橇下面的铁条与雪面之间的摩擦系数为0.02)所以,当雪橇从雪山上滑下来时,它所得到的动能会全部用于克服摩擦力。而当动能消耗完时,它就会停止滑行。
要想计算出雪橇在水平方向上滑行的距离,必须先弄清楚它从雪山上滑下来时得到的动能是多大。如 图 所示,假设雪橇从高度为AC的地方滑下来。由图可知,AC的长度正好是AB的一半(因为∠ABC=30°),所以AC=6米。我们假设雪橇的重力为P,那么当雪橇滑到水平面时,如果不考虑摩擦力,它得到的动能就是6P公斤米。至于雪橇的重力P,我们可以把它分解为两个分力:一个是跟AB垂直的力Q,一个是与AB平行的力R。由于摩擦系数是0.02,力Q等于Pcos30°,即0.87P,所以克服摩擦力消耗的动能为:
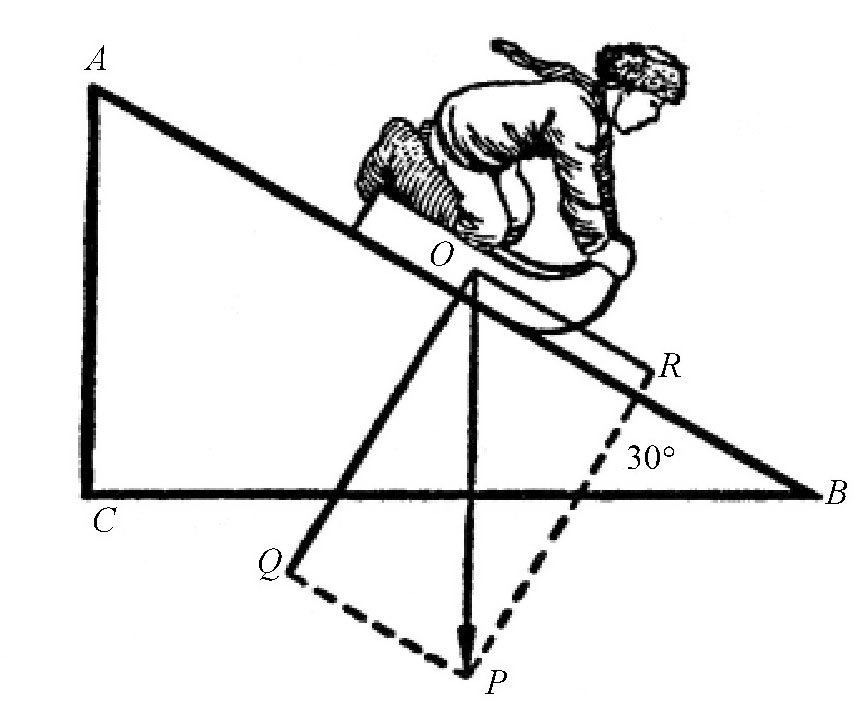
图 雪橇能滑多远?
0.02×0.87P×12=0.21P(公斤米)
所以,这只雪橇得到的实际动能为:
6P-0.21P=5.79P(公斤米)
根据题意,雪橇滑下来后,将沿着水平方向滑行。假设它一共滑行了x米,那么它克服摩擦力所消耗的功就是0.02Px公斤米。于是,我们可以得到方程式:
0.02Px=5.79P
可得:
x≈290(米)
也就是说,这只雪橇从雪山上滑下来后,将继续沿着水平方向滑行290米后才会停下来。
