一笔钱存到银行里,每年都会把利息并到本金中。这样归并的次数越多,这笔钱增长的速度就越快,因为可以产生利息的钱数变多了。来看一个简单的例子。假设存进去100卢布,银行的年利率是100%,一年结束后再把利息并到本金中,那么一年后,这笔钱将变成200卢布。要是每半年就把利息并到本金中,那么一年后,这笔钱将变成多少呢?首先半年后的总钱数为
100×1.5=150(卢布)
又过了半年后,总钱数为
150×1.5=225(卢布)
如果归并利息间隔的时间再少一些,比如说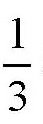
年,那么一年后,这笔钱将变成
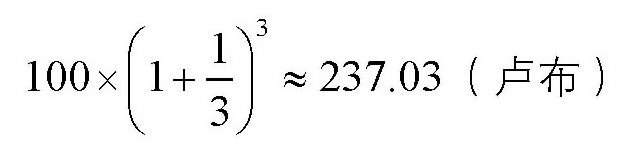
如果再缩短一些,比如0.1年、0.01年、0.001年,那么一年后,这100卢布将分别变成:
100×(1+0.1)10≈259.37(卢布)
100×(1+0.01)100≈270.48(卢布)
100×(1+0.001)1000≈271.69(卢布)
通过高等数学的方法可以证明,会得到一个极限值,也就是说,即便利息并到本金中的时间无限缩短,这100元最后也不会无限增加,而是会达到一个极限,大概是271.83元。即如果年利率是100%,那么不管把利息并到本金的时间缩到多么短,最后得到的钱数也不可能多于本金的2.7183倍。
