【题目】如图所示,人们想在这条河边建一座水塔,通过水管把水输送到旁边的村庄A和村庄B。请问,应该选择在哪个地方建水塔,才能使水管到村庄A和村庄B的总长度最短?
【解答】我们可以把这个题目改为:在河边寻找一个点,使这个点到点A和点B的距离之和最小。如图所示,假设这条路线是ACB。如果把这个图沿着CN折起来,在河的另一边,我们得到了点B′。已知CB′=CB。假设ACB就是我们需要的最短路线,也就是说,ACB′比任何一条从点A到点B′的路线(比如,ADB′)都短。那么,只要找出点A和B′的连线与河边的交点就可以了,这个点就是所求的点。这样,只要再连接点B和C,就可以得到这段最短的路线ACB了。
如图所示,过点C作垂直于CN的直线PQ,那么这条垂线PQ跟AC和BC的夹角∠ACP和∠BCP应该是相等的,而且等于∠B′CQ,即:∠ACP=∠B′CQ=∠BCP。我们都知道,这正是光线的反射定律:入射角等于反射角。光线在某个平面上反射时,选择的路径是最
图 水塔与村庄位置图示。
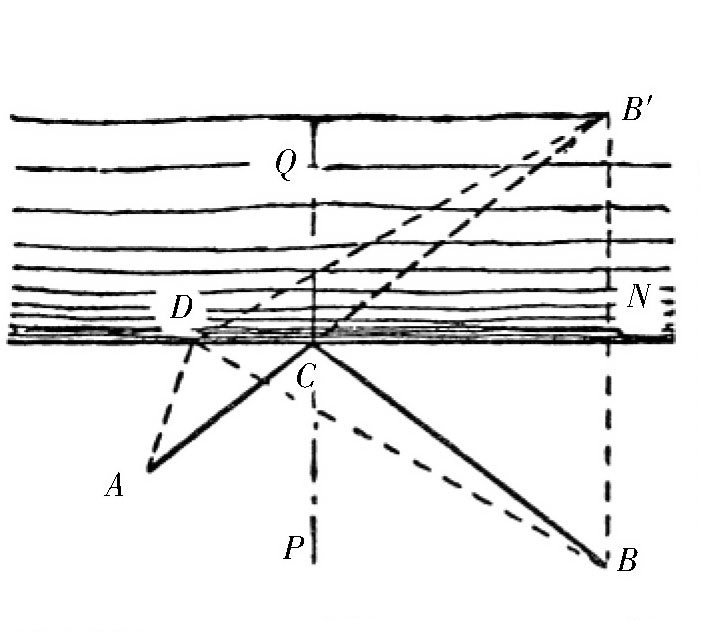
图 最佳水塔位置的图示。
11俄顷≈1.092540公顷
21俄里≈1.0668公里
31平方俄里≈104.16俄顷
