【题目】如果已知三角形3个边长的总和,那么,在什么情况下,这个三角形的面积最大?
前文中,我们提到过,这个三角形必定是等边三角形,那么,如何证明这一结论呢?
【解答】根据题目,我们假设三角形的3条边的边长分别是a、b、c,它们的和为2p,即a+b+c=2p,根据几何学原理,我们知道,三角形的面积S为:
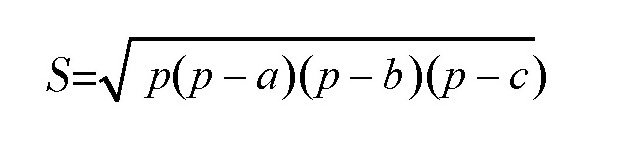
两边平方,得:
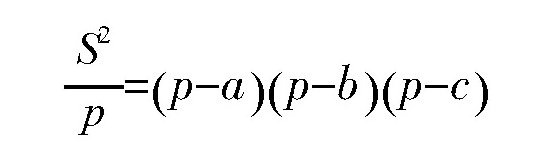
根据题意,p是三角形的半个周长,是一个定值,所以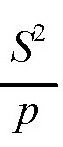
取得最大值的时候,面积S就取得了最大值。所以,问题就变成了求(p-a)(p-b)(p-c)的最大值了。也就是(p-a)+(p-b)+(p-c)在什么时候取得最大值的问题。
因为a+b+c=2p,所以:
(p-a)+(p-b)+(p-c)=3p-(a+b+c)=p
从上式可以看出,这三个数的和是一个定值p,所以,当它们三个相等的时候,它们的乘积最大,即:
p-a=p-b=p-c
所以,我们可以得到:
a=b=c
也就是说,在所有周长相等的三角形中,等边三角形的面积最大。
