下面我们来讨论如何判断一个数是否能被19整除。首先给出结论,然后进行证明。
一个数能被19整除的充分必要条件是:这个数划去个位数字之外的数加上个位数字的2倍,得到的结果是19的倍数。
【解答】对于任意的数N,都可以表示为
N=10x+y
其中,x表示这个数除了个位数字之外的数,y表示个位数字。下面来证明,N能被19整除的充分必要条件是
N′=x+2y
是19的倍数。
在上式的两边都乘以10,并减去N,则有
10N′N=10(x+2y)(10x+y)=19y
可以看出,如果N′为19的倍数,则
N=10N′19y
也能被19整除;反之,如果N能被19整除,则
10N′=N+19y
就是19的倍数,那么N′就能被19整除。
举例来说,用上面的方法判定数47045881是否能被19整除。
如下所示,我们可以连续使用上面的判定方法:
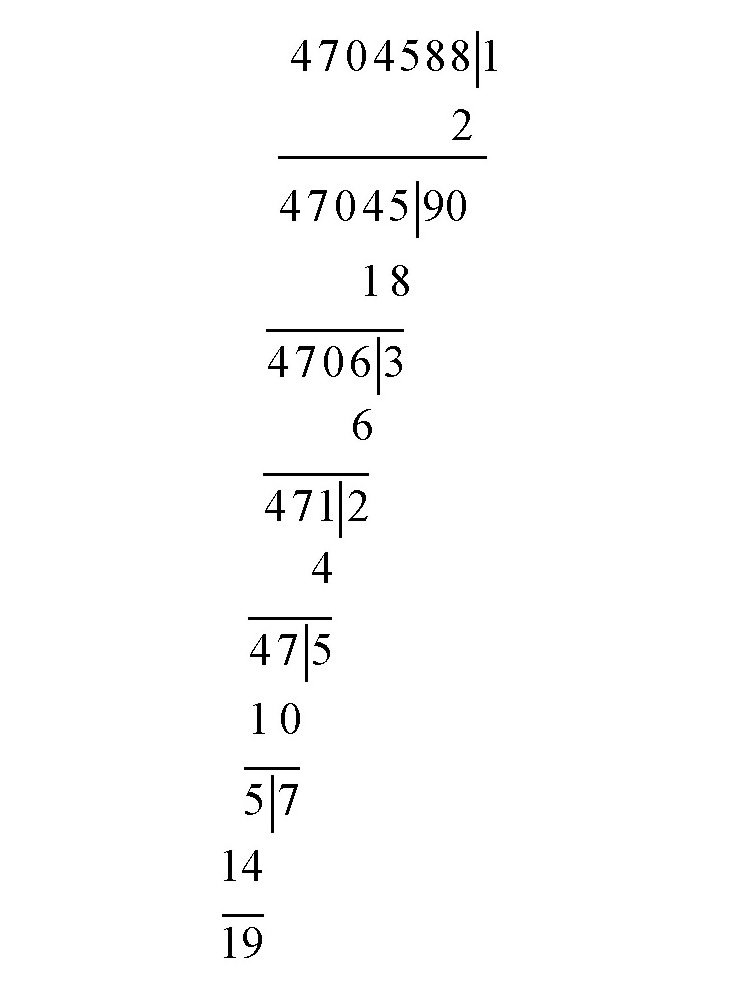
很明显,19能被19整除,所以47045881能被19整除。
同样的方法,我们可以得出:57,475,4712,47063,470459,4704590,47045881都能被19整除。
