【题目】一个风筝为扇形,它的周长是固定的,当它是什么形状时面积最大?
【解答】这个题目实际上是求:对于周长为定值的扇形,弧长和半径分别取多大时,它的面积最大。
如图所示,设扇形的半径为x,弧长为y,则它的周长l为
l=2x+y
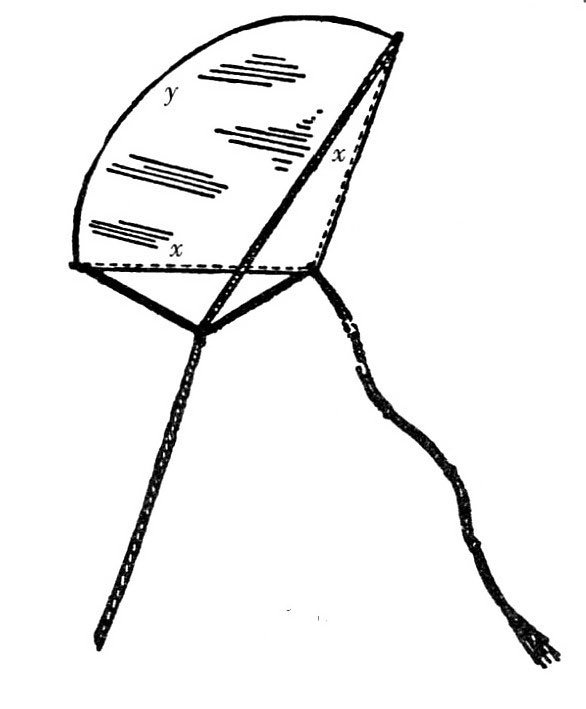
所以,它的面积为
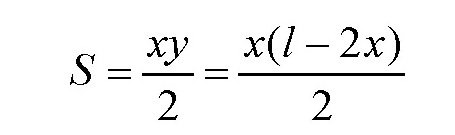
题目即求:当x取何值的时候,S取最大值。由于2x+(l-2x)=l为定值,所以,2x(l-2x)在2x=(l-2x)时取最大值。换句话说,当
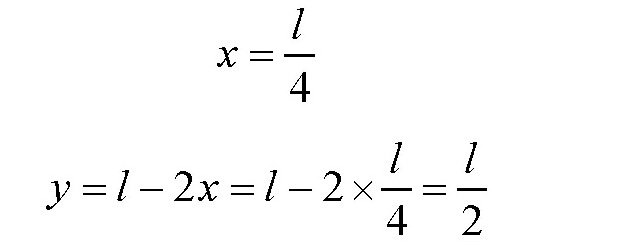
时,2x(l2x)取最大值,也就是x(l2x)取最大值,从而S取最大值。
综上所述,对于周长为定值的扇形,当半径为弧长的一半时,它的面积最大。此时,还可以进一步求出扇形的角大概为115°,约为2弧度。当然,这样的风筝是否可以飞起来,不是这里需要讨论的问题。
