用方格纸推导公式

级数问题的历史可以追溯到5000年前，但是在学校教育中出现却是很久以后的事。200多年前，马格尼茨基出版了一本教材，其中提到了级数。不过，教材中并没有出现计算级数的公式。关于级数的求和，可以通过方格纸进行推算。在方格纸上，可以把级数表示为台阶式的图形。如图所示，这个图形表示的级数为

2，5，8，11，14

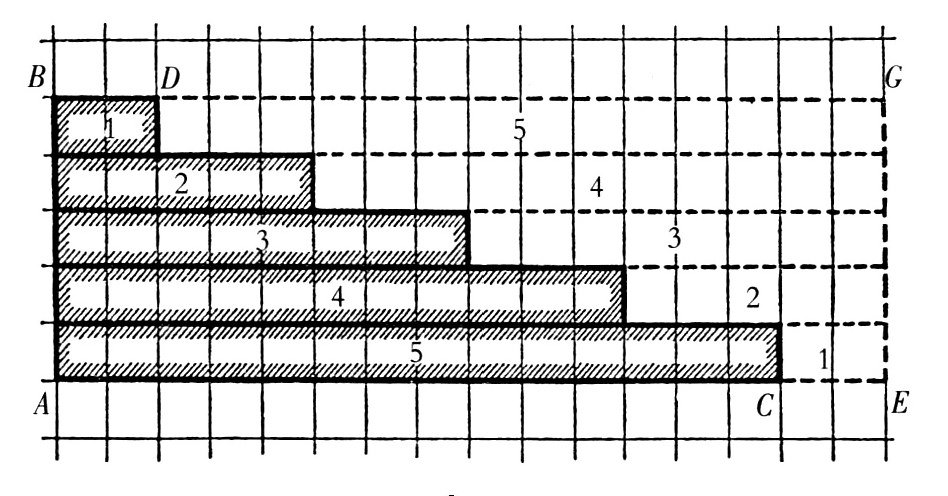
把原来的阶梯式图形扩展为矩形ABGE，这样我们就得到两个全等的图形，即ABDC和GECD，它们的面积都表示该级数的各项之和。也就是说，级数的各项之和等于平行四边形ABGE面积的一半。而平行四边形ABGE的面积

S_ABGE(AC+CE)=×AB＝80

需要注意的是，（AC+CE）表示级数的首项和末项之和，AB表示级数的项数。所以

2S＝首项和末项之和×项数

从而