【题目】一共有31只母鸡,按照每只鸡每周吃一斗的量准备了一批饲料。如果每周都减少一只母鸡,那么最初准备的饲料可以维持的时间正好是原计划的两倍。
请问,最初准备的饲料是多少?这些饲料原计划维持多长时间?
【解答】设最初准备的饲料为x斗,原计划维持y周的时间。显然有下面的关系
x=31y
如果每周都减少一只母鸡,则第一周消耗饲料31斗,第二周消耗饲料30斗,第三周消耗饲料29斗,……,第2y周消耗饲料(312y+1)斗
显然,这是一个项数为2y的级数,它的首项为31,末项为(31-2y+1),它们的和即为原来饲料的储存总量x。所以
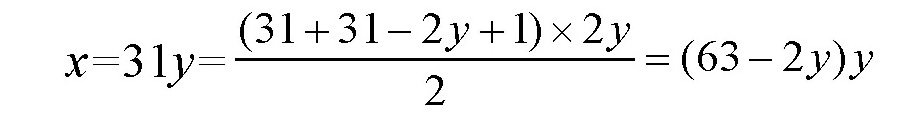
即
(63-2y)y=31y
很明显,y不等于0,所以可以约去,得出
y=16
于是
x=496
即最初准备的饲料为496斗,原计划维持16周的时间。
