【题】在不同的,开普勒第三定律会有不同的表述。在一些这样说道:行星和彗星公转周期的平方等于它们公转轨道长半轴的立方。另一些则这样表述:行星和彗星公转周期的平方等于它们离太阳距离的立方。那么你认为上面哪一种表述是正确的呢?

【解】事实上,轨道长半轴和行星距离太阳的平均距离这两种表述都是正确的。只不过它是行星绕太阳运行轨道各点距太阳距离的算术平均值,而不是行星距太阳最远距离和最近距离的算术平均值。图130为行星与太阳平均距离的计算方法,当太阳在焦点F1的位置,行星依次位于a,b,c,d等位置时,行星距太阳的平均距离可以通过把各轨道点距焦点F1的距离F1a,F1b,F1c,F1d等相加然后再除以所选取的轨道点数计算出来。通过计算可得出这个值等于长轴的一半。
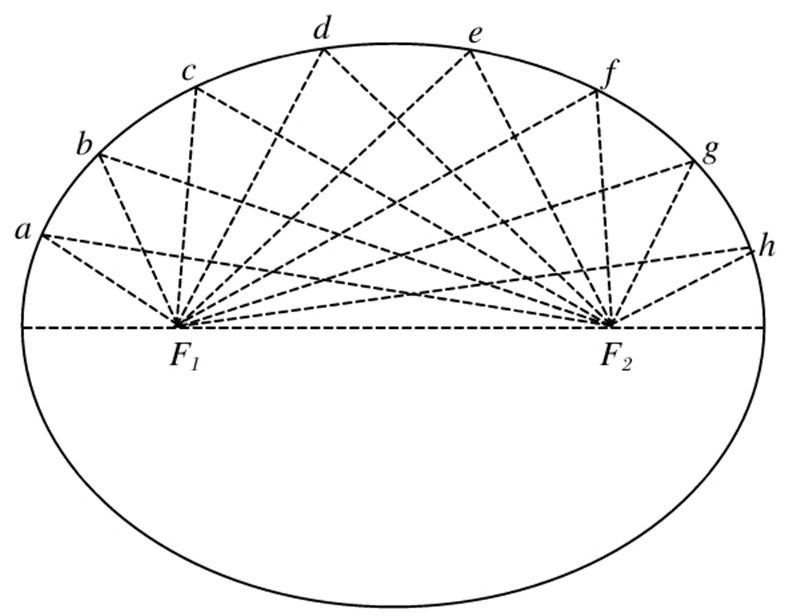
通过下面可以证明。假设取轨道上n点,由此就有n个距离。根据椭圆曲线的性质,把焦点F2与所有的点相连,各点距两个焦点的距离之和就等于2a,所以:
aF1+aF2=2a
bF1+bF2=2a
cF1+cF2=2a
……
分别将等式左边所有项和右边所有项相加可得出:
(aF1+bF1+cF1+…)+(aF2+bF2+cF2+…)=2an
假如n无穷大,在椭圆曲线里由于两个括号里的表达式是对称的,而每个括号里的表达式都是所有行星位置距焦点(即距太阳距离)的距离之和,这个总和我们用S表示。可以得出:
2S=2an
从而得到:
S/n=a
其中,S/n是表示行星距太阳的平均值,a是表示行星轨道长轴。也就是说,所有的行星距离太阳的平均值与行星轨道长半轴是相等的。
