【题】我们在给浴缸排水的时候,会发现有旋涡出现在排水管附近。那么你知道旋涡会按照顺时针旋转还是按照逆时针旋转?

【解】在几年前,这个命题中所提出的问题就引起了著名的数学家格拉维院士的注意。他在曾写道:“如果借助水槽底部的排水孔排水,那么在排水孔上部就会形成一个漏斗形的旋涡,这个旋涡在北半球沿逆时针方向旋转,而在南半球就会沿另一个方向旋转。每个读者都可以放掉浴缸中的水,自己来检验上述观点是否正确。为了更好地观察旋涡的旋转方向,可以朝水中扔些纸屑。只要在家中用最简单的方法就能操作一个验证地球自转的有效实验。”
由此,格拉维还得出了一些有实用性的结论:“一些有关涡轮机的重要结论就可以通过上述分析得出。卧式涡轮机如果是沿逆时针方向旋转,那么涡轮机做功就能够受到地球自转的帮助;反之,涡轮机如果是沿顺时针方向旋转,那么它做功就会受到地球自转的阻碍。”
“因此在预订新涡轮机时,为了涡轮机沿着有利的方向旋转,应该严格要求轮叶的倾斜方向。”这是格拉维最后的总结。
似乎感觉这些推断很正确。气旋产生旋涡状的扭曲以及铁路上右边的铁轨磨损更加严重等,这些我们都知道是地球自转导致的。那么水槽中的水漏斗和涡轮机会受到地球自转的影响,是可以想象得到的。
但是对于最初的印象我们不能完全地相信。因为我们可以很容易地将浴缸排水孔附近水漏斗的观察结果检测出来,而结果告诉我们并不是像上面所述的那样:水旋涡的旋转有时是沿着逆时针方向的,而有时是沿着顺时针方向的。特别是当参与实验的是不同的浴缸,而不是同一个浴缸的时候,不但运动方向不稳定,而且连运动趋势也不明显。
运算得出的结果和观察情况是相同的。通过结果可知,此时产生的回转(“科里奥利索夫”)加速度的值相当小。我们假设a表示回转加速度,v表示物体的运动速度,w表示地球自转的角速度,φ表示地球纬度。运用公式如下:
a=2vwsinφ
比如,水流速度在圣彼得堡所处的纬度上是1米/秒,那么v=1(米/秒),w=2π/86 400,sinφ=sin60°=0.87,则
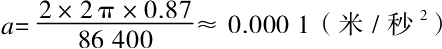
通过上面的公式可知,由于地球的重力加速度是9.8米/秒2,所以回旋加速度就是重力加速度的十万分之一。也就是说,所形成的作用力是旋转的水旋涡重力的十万分之一。显而易见,只要相对于排水孔的位置,水槽底部装置有任何一点不对称都会对水流的方向造成影响,而且相对于地球自转对它的影响来说,这个影响要大得多。多次对同一浴缸的排水情况进行观察表明:虽然旋转方向是一样的,但是由于确保旋涡方向的前提条件不是地球的自转,而是浴缸底部的形状和它表面的粗糙度,所以对预期设想的旋转规律来说,这一点却并不能将其证实。
换言之,我们应该这样来回答这个问题:对于排水孔附近的水旋涡的旋转方向是无法预知的;这个方向不是通过计算得出的,而是由具体的情况来决定。
而且通过运算我们可以知道,相比排水孔附近形成的旋涡直径,在地球海洋上形成的水旋涡直径则要大得多。比如,流速在圣彼得堡市的纬度上是1米/秒,该旋涡的直径就达到18米;而当速度是0.5米/秒的时候,直径就是9米(与流速成正比)。
下面我们继续分析一下涡轮机做功时受到的地球自转的预期影响。受地球自转的影响,每个旋转着的轮状物不仅轴线与地轴平行,而且它们的旋转方向也相同(见图75旋涡运动图解:上面为浴缸流水的情形,下面为旋转方向。)。这点从理论上是可以证实的。“所有绕轴线旋转的物体当前都处于运动之中,其轴线总是有偏向北极星的趋势;但无论旋转的物体怎样极力挣脱托架,这个趋势还是不能实现。”这段话来源于别利所写的一本关于回旋体的书。
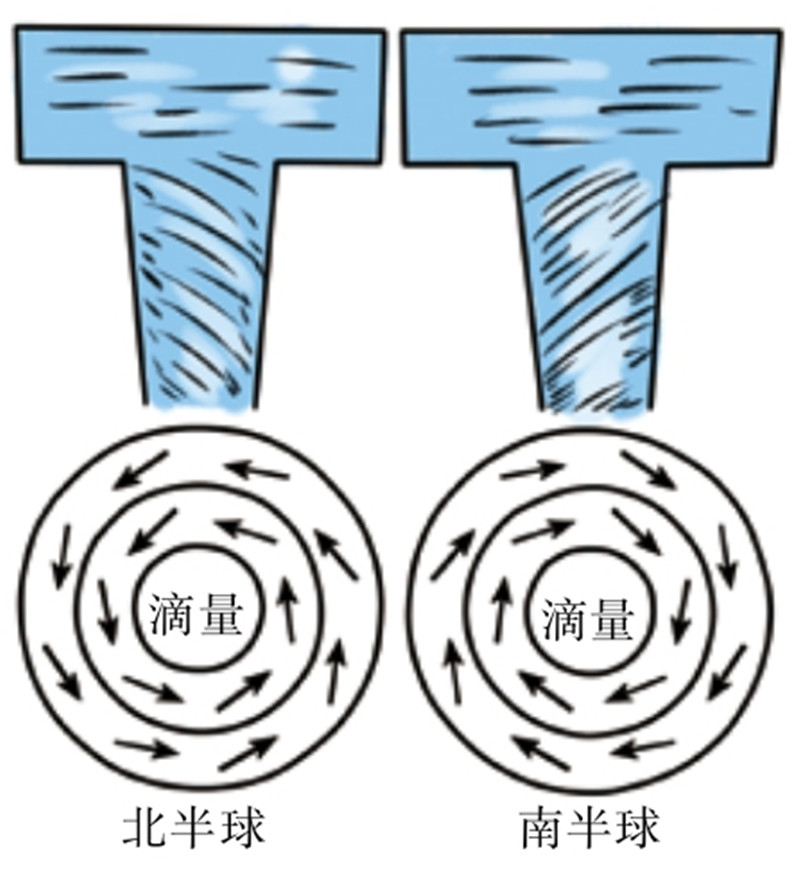
浴缸排水时所形成的水旋涡受地球自转的作用力影响是非常小的。也就是说,地球自转的作用力不到重力的十万分之一。所以,相对于地球自转对它的影响来说,只要存在着涡轮机旋转体外壳的不均质性这个特点,对于水旋涡的作用力它就要起主要的作用。那么最终可以证明地球自转“能够帮助旋转装置做功”(格拉维院士在上文中所提到的)这一观点是不再具有说服力了。
