【题】(1)8分钟可以将一个内壁垂直的浴缸放满水,关闭水龙头,通过排水孔将浴缸中的水排空则需要12分钟,那么在注入水的同时打开排水孔的情况下,浴缸需要多长时间才能够盛满水?
(2)浴缸在8分钟内就可以放满水;如果浴缸的水在关闭水龙头同时打开排水孔的情况下还是在8分钟内排空,那么在一昼夜的时间内不间断地向空浴缸内注水的同时打开排水孔,到最后会有多少水留在浴缸内?
(3)如果还是8分钟可以将浴缸注满水,但是仅用6分钟的时间就可以将水排完,请解答一下上述问题。
(4)如果需要半个小时才能将浴缸注满水,而仅需要5分钟就能将水排完,请再次解答一下上述问题。
(5)与注水时间相比,浴缸排水所需要的时间要短一些。假如给空浴缸注水和排水同时进行,那么还会有一点水留存在浴缸中吗?
为降低解题难度,我们可以忽略液体对排水孔边缘的摩擦力和流动液体的压力。

【解】针对上述5个问题,下面分别列出了正确和错误两种不同答案。
(1)浴缸注满水需要24分钟。:(1)浴缸永远都注不满水。
(2)浴缸最后是空的。:(2)浴缸中的水注到14高。
(3)浴缸最后是空的。:(3)浴缸中的水注到694高。
(4)浴缸最后是空的。:(4)浴缸中的水注到1414高。
(5)浴缸中最后一点水也没有剩下。:(5)浴缸中还剩下一点水。
肯定会有不少人认为左边的答案是正确的,但实际上右边的答案才是最终的正确答案。
下面我们分别对这些问题进行分析。
第(1)题,比起排水时间,浴缸的注水时间要短。我们可以通过计算来大体得出注满水所需要的时间:每分钟注入的水是浴缸容量的1/8,而排出的水是它的1/12;换言之,浴缸每分钟所增加的水的体积是整个浴缸容量的1/24,也就是1/8-1/12=1/24。那么浴缸在24分钟之后就会注满水这个答案似乎应该很明了,但是我们可以看到右边正确的答案显示的是,浴缸永远都注不满水。这又是为什么呢?
第(2)题中,浴缸的注水时间和排水时间是相等的。换句话说,进入到浴缸中的水的体积和排出的水的体积在每分钟内都是相等的。这样看来,无论是多长的注水时间,浴缸中都应该不会有一滴水留存。但是右边正确的答案却是,浴缸中的水注到1/4高。
(3)(4)和(5)这三种情况,在感觉上应该是浴缸中注入的水没有排出的水多,但是右边正确答案却是,此时的浴缸中还是有水剩下的。
综上所述,是不是感觉我们提供的正确答案似乎很荒谬啊?对于这些答案,读者们可能也经过长时间的讨论且也有自己的看法。那么下面我们先来看一下第(1)个问题。
格伦阿列克桑德利斯基提出了著名的浴缸问题(如图,两千年来,这个问题一直在中学算术习题集之中出现),而上面这些问题则是浴缸问题的变形。对于这个问题的解答从物理学角度来看,是错误的。虽然被普遍接受,但是却是一个以错误的假设为前提的解答方案。而这个错误前提就是只要水龙头的水流适当,水就会从水面不断降低的贮槽中流出来。而依据物理原理,水流速度会随着水面的降低而减缓。所以这个假设与物理原理是矛盾的。因此,认为整个浴缸如果需要12分钟可以排完水,那么每分钟排出的水就等于浴缸容量的1/12,这个中学生们在算术课上经常会学到的知识点是错误的。实际上与上述论述是完全不同的:每分钟的流量在最初水面较高的时候会大于浴缸容量的1/12;而在接下来这个数量会不断减小,直到水平面很低的时候,每分钟的流量就小于浴缸容量的1/12。换言之,每分钟平均的水流量是与浴缸容量的1/12相等的,但是却不是每一分钟的流量都与它的1/12正好相等,不是大于它,就是小于它。其实马克·吐温曾经给我们讲过的笑话故事中的怀表就与浴缸排水的例子十分类似:怀表一昼夜应该转动多少圈,它就勤恳地运转了多少圈,平均下来走得十分准。但是怀表在上半夜会走得相当快,而在下半夜的时候又会走得很缓慢。想要解决这个问题,我们可以利用水流的平均速度,也就是如何利用马克·吐温的这个怀表来计时。

在解答这个问题时我们发现,应该考虑更多的不是算术习题中简化后的情况,而是自然属性的现实情况。这样就会有不一样的结果了。假如最初注水是在水面还不太高的时候,流量小于浴缸容量的1/12,而再注水是在水面上升到一定高度后,这时的流量就大于1/12,甚至有可能会达到浴缸容量的1/8。换言之,排水量在水注满之前就等于进水量了。这时的水面高度就不再上升:排水孔会将所有水龙头流出来的水都流走。相比浴缸顶面,水面总是低于它的。所以这一点即无论如何浴缸中的水永远是注不满的就很好理解了。而上述分析通过下面的数学运算就可以证实。
第(2)题,注水和排水时间都是8分钟。刚开始注水时,水面较低,每分钟的进水量是浴缸容量的1/8,流量方面我们在上面已经分析过,是小于1/8的。所以,水面会上升,一直到进水量与排水量相等。因此浴缸不会是空的:里面应该是有一部分水存留的。由此我们可以做出推断,浴缸中的水面高度在注水时间与排水时间相等的时候为整个浴缸高度的1/4。显而易见,这个问题的解答也是正确的。
(3)(4)和(5)这三种情况,排水时间与注水时间相比都是要短的。不论进水量是多少,整个浴缸的水是不可能被注满的,但是总是会存留一部分水。所以,我们对这三个问题的答案正确性也就没有什么疑问了。我们现在可以回想一下,因为水面较低的情况下,最初水龙头中水的流速是不可能太快的,即流速是很小的;而且不论流速大小,在流速均匀的情况下,水面会继续下降。也就是说,水槽中无论怎样都会有部分水残留下来,即使水量很少。换言之,任何一个带孔的柱状物只要进水时水流匀速,其中都会有部分水残留下来。
上述问题我们现在从数学角度来分析。实际上我们看到,那个浴缸问题(两千多年来作为中学生基础算术题)远远超过了算术初学者所能解答的范围。
假如用H表示浴缸蓄满时液体的高度,T表示浴缸注满所需要的时间,t表示蓄满的浴缸排完水所需要的时间,S表示浴缸截面,c表示排水孔截面,w表示浴缸中液面下降的速度,v表示排除液体的速度,l表示排水孔打开时水面的高度。假如打开排水孔,同时给圆柱形浴缸注水,那么我们研究一下注水时间T、排水时间t以及液体所达到的高度l之间的关系。
假如液面每秒钟下降的速度为w,那么排水孔在这一秒钟内流出的液体体积Sw就与液柱的体积cv相等,公式如下:
Sw=cv
由此得出:
w=cv/S
根据著名的托里拆利公式,可以得出从排水孔中流出的液体的速度,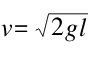
,这个公式里面的l表示液面高度,g表示重力加速度。另一方面,液面在排水孔关闭时上升的速度w等于H/T。只有在液面下降的速度等于上升的速度时,才能保持这个平面固定,即存在着这样一个等式:
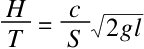
所以固定下来的高度l就等于:

这就是浴缸在打开排水孔后注水时的最大高度。可以通过代入S、c、g的大小来简化该公式。内壁垂直的浴缸,在打开水龙头后,其内的液面下降是匀变速l运动,也就是它的初始速度是w,末尾速度等于零。我们可以通过下列的方程式把这个运动的加速度a计算出来:
w2=2al
所以
a=w2/2l
然后将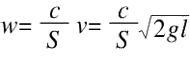
这个表达式代入,得出
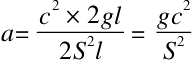
这样,对于上述的运动情况来说:

进一步得出
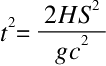
将其代入式子①中,最后得出
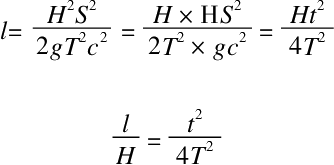
通过上述情况我们可以看出,浴缸液面高度占据了浴缸高度的一部分;通过下列公式可以将该高度计算出来:
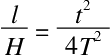
值得一提的是,浴缸和排水孔的形状、截面大小以及加速度g都不是影响液面的最大高度的因素。也就是说,液面的最大高度与上面这些都是没有任何关系的。所以,液面无论在火星、木星还是在地球上都是相同的。液体高度H在浴缸蓄满后就是在t秒钟内任何一个下降液面的高度。
对于上述问题,下面我们运用推导出来的公式来解决一下。
第(1)题,T注水所需要的时间为8分钟,t排水所需要的时间为12分钟。最大高度l占浴缸高度H的比例就是:
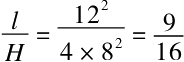
无论向浴缸注水时间有多长,浴缸只能注到9/16,高度都不会再上升。
第(2)题,此时,T和t都是8分钟,浴缸只能注到1/4。
第(3)题,这道题中注水时间T是8分钟,排水时间t为6分钟,则
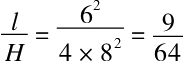
浴缸只能注到9/64的位置。
第(4)题,已知T是30分钟,t是5分钟,则
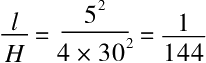
所以只能注到浴缸1/144的位置。
第(5)题,已知t<T,通过公式

所得到的式子只有在下面两种情况下才能等于零。
第一种:t=0,T≠0。这说明,在瞬间浴缸排完水这种情况是不太现实的。
第二种:t=0,T→∞。这说明,浴缸在关闭了排水孔后永远都注不满水,也就是说,流量是为零的,水龙头完全不出水。这种情况在实际中就等于水龙头是关闭的。
所以,只要打开水龙头,瞬间内浴缸不会排空水,l/H就不会为零,因此总会有一部分水残留在浴缸中。
当l=H;t2/4T2=1;t2=4T2;t=2T这几种情况下,将排水孔打开,浴缸还是有可能注满水的。
换言之,浴缸在注水时间是排水时间的二分之一的条件下,在打开排水孔的情况下仍然可以注满水。
要达到一个固定的液面高度需要多长时间呢?解决这个问题需要运用到积分学知识,只是单纯依靠基础数学方法是不行的。下面我们列举出了运算过程,读者可以根据自己的实际情况看一下。
假如用液面在关闭排水孔时上升的速度H/T与浴缸在未注满时液面下降的速度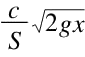
(x表示此时液面的高度)相减,就可以得到注水浴缸在打开排水孔后液面上升的速度:
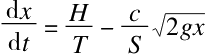
得出
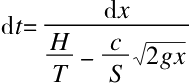
液面达到x=h这个高度所用的时间我们用Θ来表示,方程式如下:
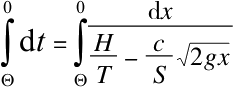
我们通过求这个方程式的积分得到计算达到高度h所需要的时间的公式如下:
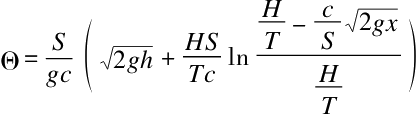
这个方程式也可以简化一下,浴缸排水时从高度h下降的速度w,从公式wS=vc和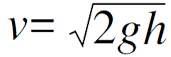
中我们可以得到:
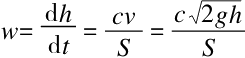
所以
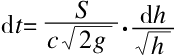
而且
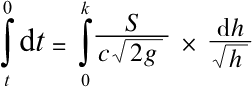
得到
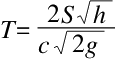
我们经过一系列的代换之后,可以得到下面这个关于Θ的公式:
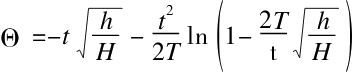
最终得出的式子,我们可以看到其中既没有浴缸截面S和排水孔截面c,也没有重力加速度g,所以注满浴缸所需要的时间无论是在哪个星球上都是一样的。
浴缸中的水什么时候才能够达到最大高度呢?回答则是:只有在无限长的时间内才能够实现,也就是说,这是不可能实现的。因为液体上升的速度随着液面不断靠近最高点一直在减小;它的速度在液体越靠近这个点的时候就会越小;而事实很明显,液面是不可能达到这个高度的,只能够去无限地接近它。这个推论很简单,而上面的结论也是在预料之中了。
但是如果想要解决实际问题,我们可以换一种提问的方式。液面达到最大高度或是只达到这个高度的百分之一,这两者是没有比较意义的。我们可以通过上述公式计算出这种接近达到所需要的时间,将h=0.99H代入,这里的l表示最大高度,得出下列公式:
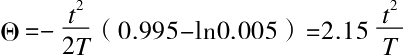
我们把这个算式应用到上面的五种情况中。
当T=8(分钟),t=12(分钟)时:
Θ=2.15×122/8=38.7(分钟)
当T=t=8(分钟)时:
Θ=2.15×82/8=17.2(分钟)
也就是说,液面在17分钟之后才达到一个固定高度。
当T=8(分钟),t=6(分钟)时:
Θ=2.15×62/8=9.7(分钟)
即液面会在约10分钟后达到一个固定高度。
当T=30(分钟),t=5(分钟)时:
Θ=2.15×52/30≈1.8(分钟)
可以看出,液面在不到两分钟的时间内就能达到最大高度。
第五种情况中,要想实现给打开排水孔的浴缸注满水,就只有在前面假设的情况下,也就是当t=2T时,这时需要的时间就是:
Θ=2.15×t2/T=4.3t=8.6T
我们关于浴缸的问题就分析到这里了。相比那些粗心大意地向初中生提“水池问题”这类算术题的出题人,要说服读者认同这个道理的过程要困难复杂得多。
