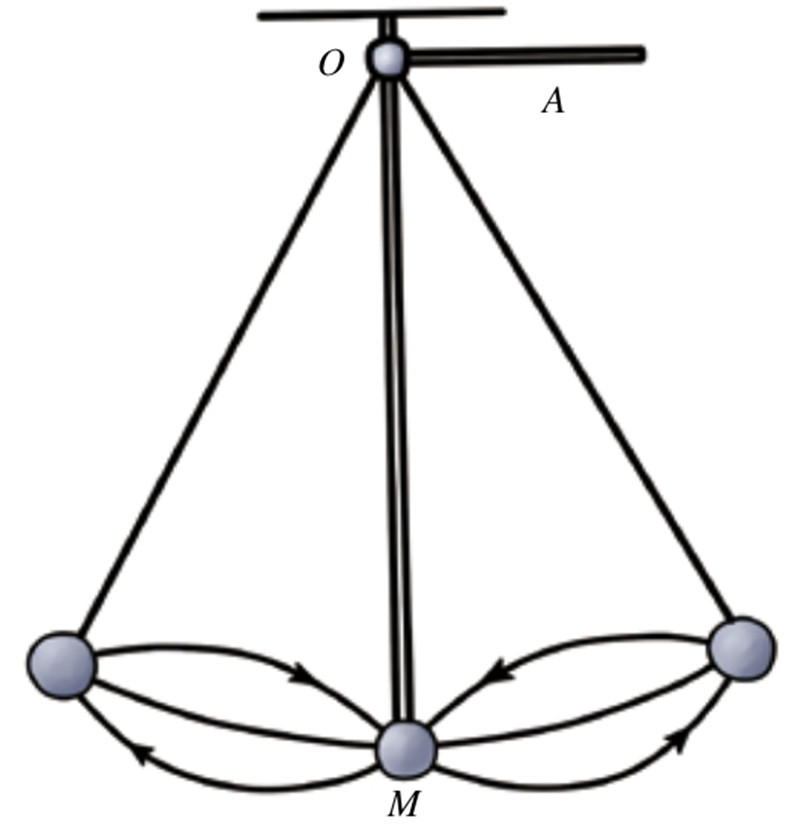
【题】如图所示,人站在秋千上,要想增加秋千的摆动幅度,可以通过一些肢体运动实现。那么这个观点是否正确,秋千中隐藏着怎样的力学原理?

【解】这个观点确实是正确的。我们站在秋千板上,要想逐步增大摆动的幅度可以借助适当的肢体运动,以达到我们想要的任何高度。对此,应该做到下面的两点。

(1)位于最高点时,保持蹲下来的这种姿势,直到秋千荡到最低点也就是秋千的绳垂直指向地面时再站起来。
(2)位于最低点时,保持身体伸直这种姿势,直到秋千荡到最高点时再俯下身去。
简单来说就是:在木板摆动的一个轮回中,做“向下时蹲下去”和“向上时站起来”这两种肢体运动。
上述方法从力学角度来说是合理的。因为在性质上,秋千类似于一只人体摆锤。在秋千上当人蹲下时,他使摆动中物体的重心放低;而当人站起来时,物体的重心又被他抬高。所以,摆锤在每个摆动轮回中交替着两次变化,它的摆长时而增大,时而减小。
那么长度发生变化的摆锤会如何摆动呢?
如图所示,假设AB是摆锤,AB?是它处于竖直状态的时候,AC?是它的最短距离。既然摆锤上的重物降落的高度为DB?,那么它应该在最远的路程内用其所集聚的动能总量将这个重物送到相同的高度。因为上升时的功不是由积聚的能量产生的,因此,这个总能量在重物从点B?升到点C?时没有减少。所以,由点C?运动到AC位置的重物在铅垂线的带动下上升时多出来的长度应该是C?H,且等于B?D。从而我们发现,最初的角a比摆锤线偏离时产生的新的角b要小。
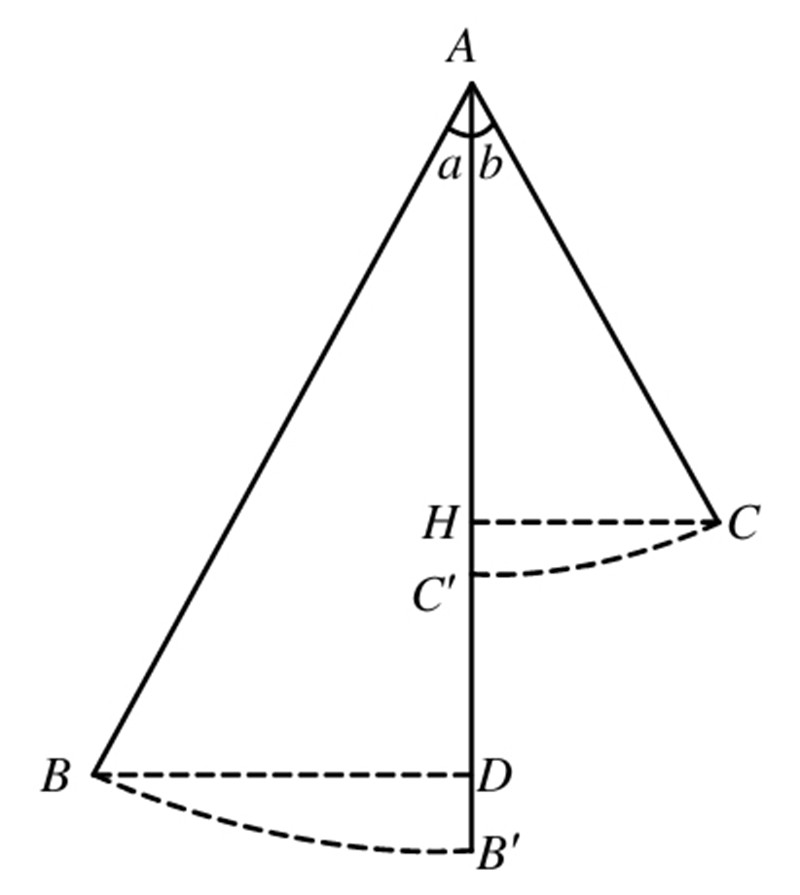
DB?=AB?-AD=AB-AB cosa=AB(1-cosa)
HC?=AC?-AH=AC-AC cosb=AC(1-cosb)
因为DB?=HC?,所以
AB(1-cosa)=AC(1-cosb)
那么
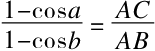
通过变换表达式1-cosa和1-cosb,可得出
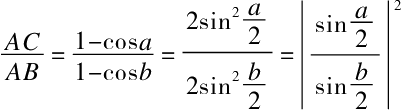
因为AC<AB,所以
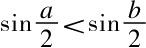
而因为两个角都是锐角,所以a<b。
所以,从竖直方向上摆锤线(和秋千绳)偏离出去的距离要比最初偏离的距离远。这就是人在木板向上运动时站起来对秋千施加的作用力的结果。
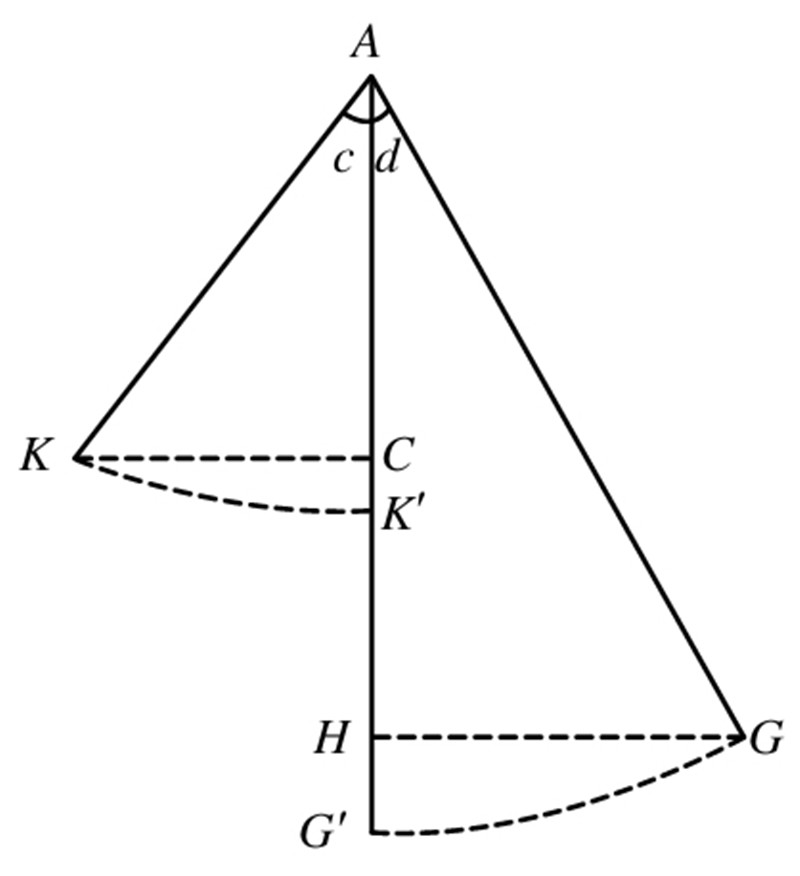
如图所示,我们再观察一下摆锤上重物的最高点到最低点,即方向的运动。需要注意的是此时摆锤的长度是增加了的:从点C降落到点G。当摆锤从位置AG运动到AG?时,下降的高度为HG?,此时在摆锤最远的运动中获得的势能总量应该将重物送到相等的高度。但是既然重物在位置AG?上,从G?升到K?,那么摆锤在最远的运动中会运动的角度就是c,这个角比角b要大,原因前面我们已经讨论过了。所以可得出c>b>a。
从上述方法我们可以看出,摆锤每摆动一次,其摆锤线和秋千绳索偏离的角度就会增加,甚至可能会逐步达到理想的高度。
同样,依靠另一种肢体运动借助这种方法就可以将秋千“刹住”,甚至最后让它完全停下来。
在《理论物理》这本,作者埃亨瓦利德教授描述了一个简单的不用借助秋千就可以验证上述观点的实验。如图所示,“把重物M拴在穿过静止吊环O的绳子上。我们可以让绳子的另一端A向左向右运动,从而周期性地变化摆锤的长度OM,如果A端的运动频率是摆锤频率的两倍,而且取得了合适的运动相位,那么就可以非常快速地拨动摆锤了。”埃亨瓦利德在这样写道。