【题】如图所示,在高精度天平的托盘上放入一个沙漏,这个沙漏每5分钟就需要上一次“发条”,并用砝码将其称重。假如将沙漏倒置过来,那么天平在5分钟内会发生的变化是上扬还是下降?

【解】人们会认为,在沙漏倒置过来的5分钟内,盛有沙漏的托盘要轻些,而且会向上扬起。因为滴漏时还没有接触到容器底面的沙粒,不会对容器底面施加压力。
但是通过实验,我们却看到这样一个结果:只有在最初的瞬间,盛有沙漏的托盘会向上晃动一下,然后天平在接下来的5分钟内都保持着平衡状态。直到最后一刻,盛有沙漏的托盘开始向下沉,最后,天平重新回到平衡的状态。

为什么天平会在5分钟内一直保持平衡状态?首先,我们分析出在每秒钟内,到达容器底端的沙粒有多少,依赖于离开沙漏瓶颈的沙粒会有多少。(思考一下,如果到达容器底端的沙粒要比离开瓶颈的沙粒多,那么那些多出来的沙粒是从哪里来的呢?反过来,缺损的沙粒又消失到哪里去了?)即沙粒在每秒钟内落到容器底部是“失重”的状态。根据处于失重状态下的沙粒落到容器底部的运动规律,我们假设h是沙粒降落的高度,g是重力加速度,t是降落的时间,得出等式
h=gt2/2
进而得
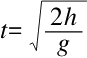
沙粒在这段时间内并没有给天平托盘施加压力。那么,在t秒钟内该托盘的重量减去沙粒的重量的差与t秒钟内作用在天平托盘上的一个向上的力(即等于沙粒的重量p)的大小是相等的。根据这个力的冲击力,我们来计算这个力的作用大小为
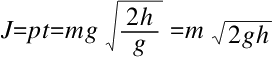
同样,一粒沙在这个时间段里滴漏到容器底部的速度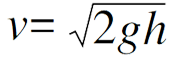
。这个滴漏的冲击力J1与沙粒运动的数量mv是相等的,即
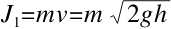
所以我们可以看出,J=J1,两个冲击力的大小是相同的。天平托盘受到不同方向上大小相等的作用力就会保持平衡。
在5分钟的第一秒时,失重的部分沙粒已经离开了容器顶部,但是在容器的底部还没有任何沙粒到达,这时,盛有沙漏的托盘就会上扬;而在接近5分钟时,在容器顶部所有的沙粒都已经离开,新的失重的沙粒已经没有了,而容器下部还发生着滴漏现象,这时盛有沙漏的托盘就会下沉。
所以只有在5分钟时间内的第一秒和最后一秒,高精度天平的平衡状态才会被打破,而其余时间托盘依然保持着平衡状态。
