【题】两个圆柱体,一个是纯铝制的,另一个外壳是铅制的,中心部分用软木填充。同时它们的重量和外表完全相同。现在,将两个圆柱体分别用纸严密地包裹起来。
试问:我们用什么样的方法才能将这两个不同材质的圆柱体分辨出来?

【解】很久之前就出现了这样的问题。这个问题在奥扎纳姆的《数理娱乐》这本还曾被这样提出过:
假设有两只球:一只是纯金的,另一只是镀金的银质实心球,两只球的大小和重量完全相等,请问,可以将金银球区分开来吗?
奥扎纳姆认为是存在着区分这两只球的方法的,虽然古代数学难题的出题人都觉得不可能解决这个问题。他在提到:“我在铜板上凿一个圆形窟窿,让两只球都能够很容易紧密地陷在其中。然后我用高于沸水的温度来分别加热两只球。由于银比金更容易膨胀,我就观察,看看哪只球的膨胀力更大些,能够先挤开这个窟窿,那么它就是银球。”
很明显,虽然这种方法理论上是正确的,但是却不适用我们所要解决的纸包裹起来的圆柱问题。不过我们也可以利用相同的原理来解决这个问题。
我们要解决这个问题的思路就来源于上个问题的分析。最简单的办法就是利用两者惯性力矩的差异去辨别圆柱。因为混合质地的圆柱的大部分质量都集中在外缘上,所以它和均质铝制圆柱的惯性是不同的。根据这一点我们就可以发现,如果让两只圆柱同时从斜坡上滚落下来,它们的平移运动速度是有差别的。
利用力学原理,均质圆柱的惯性力矩k相对于纵轴来说就等于
k=mr2/2
相对于均质圆柱计算的简单,非均质圆柱运算就要复杂一些。首先,我们要将软木圆柱部分的质量和半径计算出来。将所求半径用x表示,整只圆柱的半径仍然是r,圆柱高度用h表示,材料的密度需要特别指出,分别是
软木 ........0.2克/立方厘米
铅 ............11.3克/立方厘米
铝 ............2.7克/立方厘米
由此等式为
0.2πx2h+11.3(πr2-πx2)h=2.7πr2h
等式表明,非均质圆柱的铅壳部分和软木圆柱部分的质量之和等于铝制圆柱的质量。简化后,我们得到的等式就是
11.1x2=8.6r2
所以
x2=0.77r2
所以混合圆柱软木部分的质量等于
0.2πx2h≈0.2π0.77r2h≈0.154πr2h
铅壳部分的质量等于
2.7πr2h - 0.154πr2h = 2.546πr2h
由此可知,两者分别占总质量的比例如下:
铅壳部分:6%
软木部分:94%
然后将混合圆柱的惯性力矩k1计算出来:它等于铅壳部分和软木部分的力矩之和。
质量为0.94m(m是铝制圆柱的质量)、半径为x和r的铅圆柱壳的惯性力矩就等于
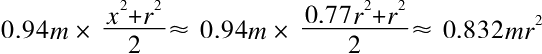
质量为0.06m、半径为x的软木圆柱的惯性力矩就等于
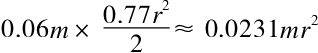
所以,混合圆柱的惯性力矩k1就等于
k1=0.832mr2+0.0231mr2≈0.86mr2
我们一样会得到滚动的圆柱的平移运动速度,和前面那个关于球体的问题是相同的。因此,均质圆柱的平移运动速度等式就是
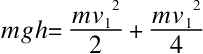
又或是
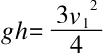
所以
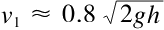
最后得出,非均质圆柱的平移运动速度就是
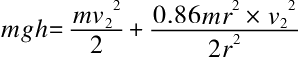
又或是
gh≈0.5v22+0.43v22=0.93v22
所以
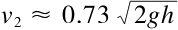
我们尝试着比较这两个速度:
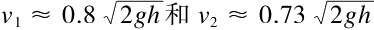
从中我们可以看出,混合圆柱比均质圆柱的平移速度小9%。依据这个结果,我们就知道与混合圆柱相比,铝制圆柱要更早地滚到坡底。
换一个问题,如果混合圆柱的铅集中在中心,而铅芯是被软木从外向内包裹着,那么,聪明的你能够分析出来此时更早滚到坡底的是哪个圆柱吗?
