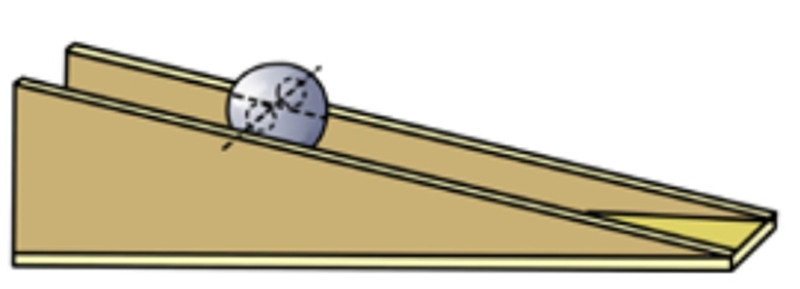
【题】(1)如图所示,两只球同时从A点开始运动:一只沿着竖直线AB自由落体,另一只沿着坡面AC滚动。其中,A点与水平地面的高度为h。那么这两只球所获得的平移速度会是一样大吗?
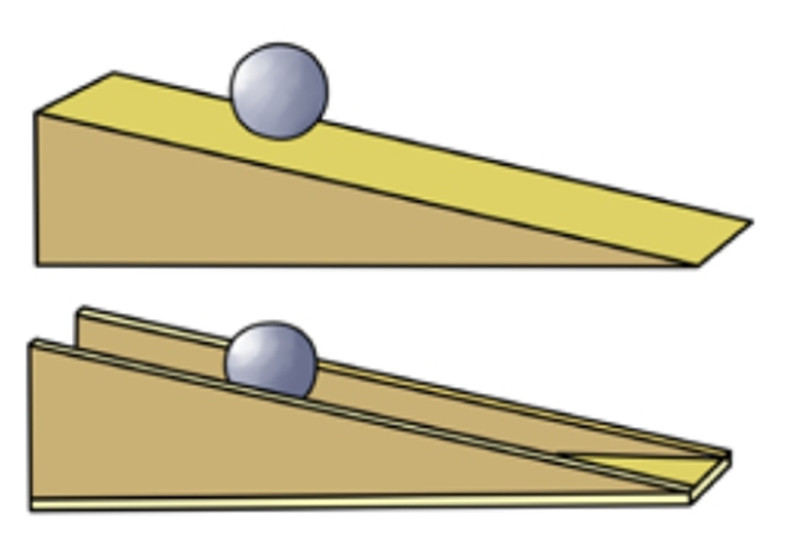
(2)如图所示,一只球沿着坡面滚动,另一只球沿着两片平行的三角木板滚动。上述两种情况中,球是一模一样的,坡面的倾斜度以及运动的高度也都是一样的。两只球会同时到达坡面的底端吗?

【解】(1)在解决这个问题之前,我们必须要弄明白:从A点竖直落下的球是只做平移运动的,但是另一只沿着平面滚动的球除了做平移运动以外,还会做旋转运动。而许多人则会常常误以为:沿着平面滚动的球只做平移运动——甚至一些中学的教科书上也会出现这种纰漏。
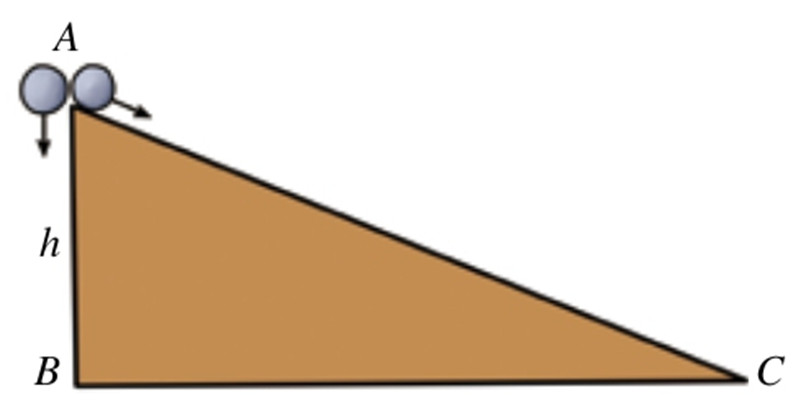
下面我们通过演算来看看,上述状况会给滚动的物体带来什么影响。
在垂直下落时,斜坡上的球的势能全部转化为平移运动的能量,我们用p表示球的重力,m表示球的质量,g表示重力加速度,v表示球的速度,得出公式
ph=mv2/2
用球的质量和重力加速度的乘积代替球的重力,得到等式
mgh=mv2/2
最后得出该球的速度为
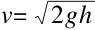
我们再来演算一下沿着坡面滚动的球的速度。因为这个球除了做平移运动,还做旋转移动,我们用v1表示平移速度,用ω表示旋转运动的角速度,用k表示惯性力矩。此时,斜坡上的球的势能ph就转化为两个动能之和:一个是速度为v1的平移运动能量,另一个则是角速度为ω的旋转运动的能量。
平移运动的能量就等于mv21/2。
旋转运动的能量等于球体惯性力矩的一半乘以球的角速度的平方,即kω2/2。
最后得到等式
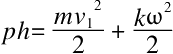
我们根据力学教材可以知道,相对于通过中心的中轴线来说,半径为r、质量为m的均质球体的惯性力矩k就等于2mr2/5。从而我们可以算出,这个平移速度是v1的球的角速度ω等于v1/r。所以,旋转运动的能量就是
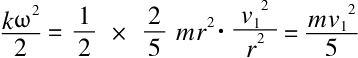
另外,用球的质量和重力加速度的乘积代替等式中球的重力p,那么
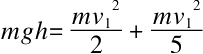
简化得出
gh=0.7v21
从而得出平移速度为
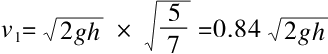
把得出来的这个速度与竖直降落的最后的速度(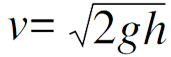
)相比较,我们可以看出这两者之间存在着很大的差异。将滚动的球(无论半径和质量)与从此高度自由落体的球做对比,前者的速度在路径的末端或任何一点上比后者的速度都要小16%。
所以很容易就能确定:在路径的任何一点上,沿着坡面滚动的球同沿着从同一高度上平面滑行的物体相比来说,前者的速度都比后者的速度小16%。
在不考虑摩擦力的情况下,滑动的球会比滚动的球少用16%的时间到达坡底。对于竖直下落的物体来说也是这样:它比滚动的球要早到坡底(时间少用16%)。
对物理史有所了解的人都知道:伽利略的物体落体定律就是通过将球放到坡槽(长度约为6米,高度为0.5~1.5米,见图41)中做实验论证得出的。而伽利略之所以能够借助坡槽正确地得出物体落体定律,就是因为:在平移运动中滚动的球的加速度是不发生变化的,是由于它的速度在坡槽的每个点上都是同一水平面上竖直下降球体速度的0.84。所经过的路程和时间之间的关系同自由降落的物体是一样的。
伽利略在其就这样写道:“我发现,如果把球体放入原槽长四分之一的槽内,那么所耗费的时间正好等于原来时间的一半……重复实验一百次,我发现所经过的路程之间的比总是时间比的平方。”
(2)首先我们看到,因为两个球体的质量相等,并且它们也是从同一高度向下落的,所以球体最初的势能是一样的。此外,还应该指出的是,沿着平面滚动的球与在木板间运动的球相比,后者碾出的圆圈形的半径要比前者小(r2<r1)。
对于沿平面滚动的球来说,同第一个问题一样,我们可以得出相同的结论:

对于在木板间运动的球来说
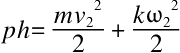
代入
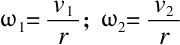
得出
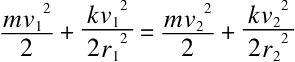
然后算出
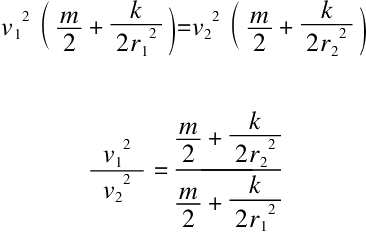
可知右边分数的分子要大于分母,因为我们前面已知r2<r1,进而得出v1>v2;所以,沿平面运动的球的速度比在木板间运动的球的速度要快,而且也更早到达坡底。
