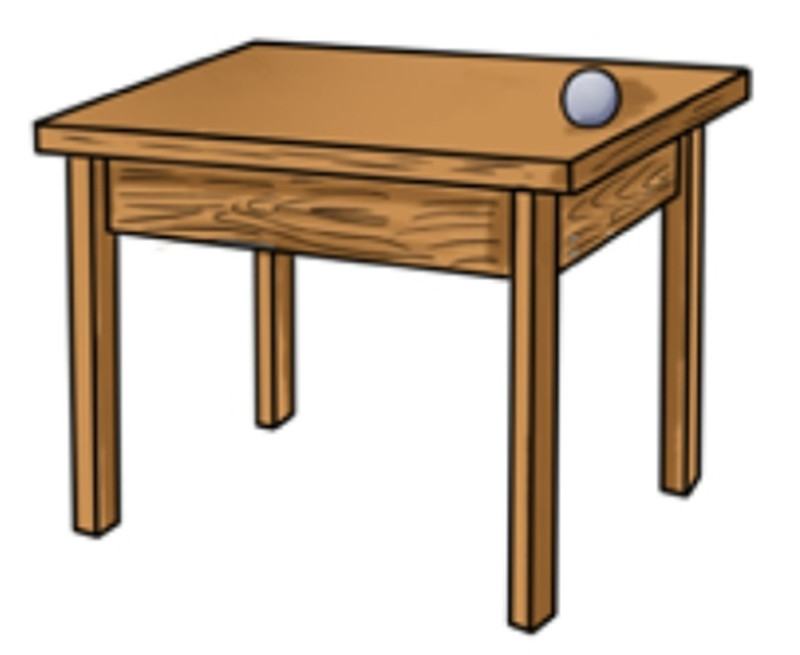
【题】如图所示,把球放到桌子的边缘,让铅垂线穿过桌子的中心并且与桌面保持严格垂直。假如桌面的摩擦力不存在,那么球在桌面上是运动的还是静止的?

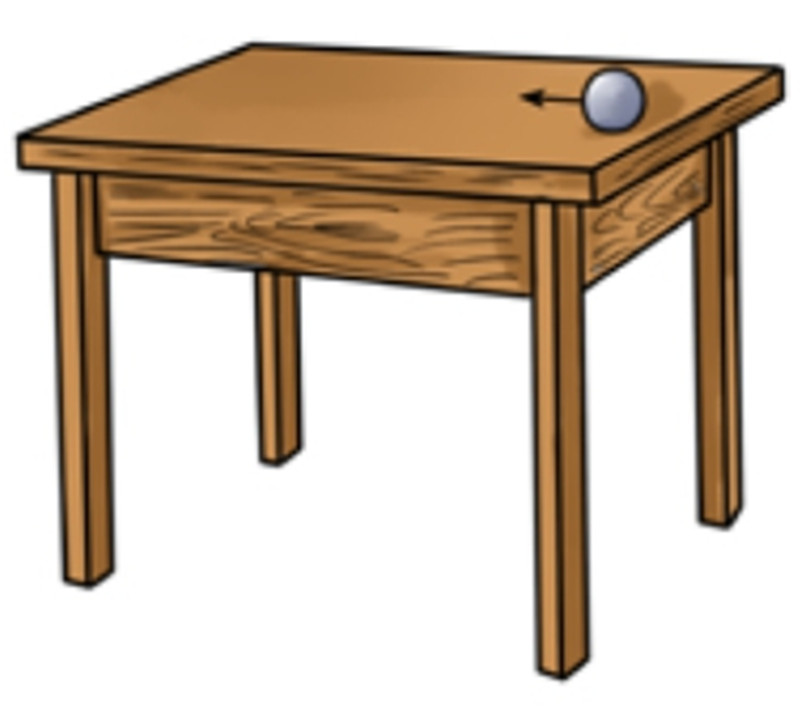
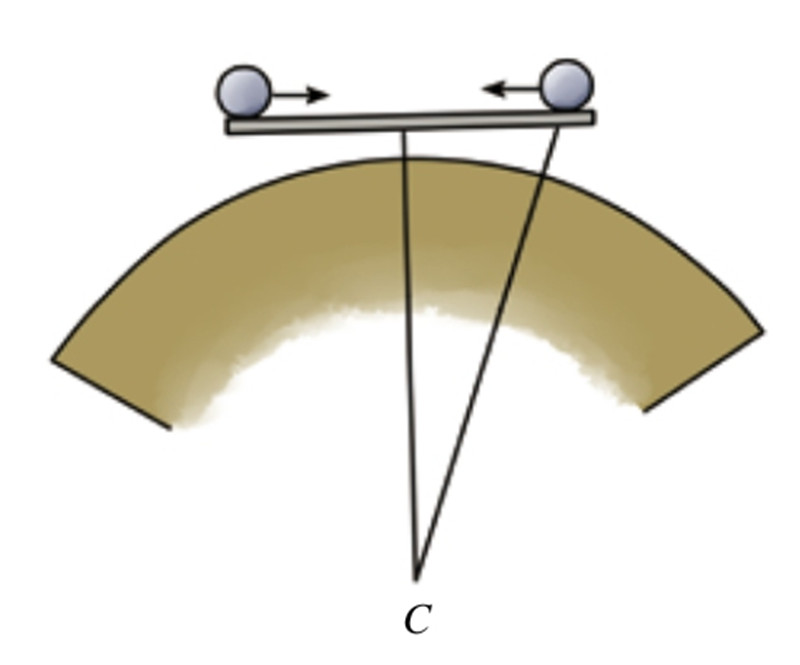
【解】假如不存在摩擦,桌子平面也是完全光滑的,那么球应该是运动的,而且还是从桌沿滑向桌心(见图35)。为什么呢?因为铅垂线是垂直穿过桌面的中心,而桌沿要比桌面中心离地心更远,也可以说是更高(虽然实际上它们两者之间相差并不明显),所以球会从桌沿滑向桌心。但是因为积蓄起来的动能会将球吸引到那个和最开始的点处于同一水平面的点上去,即另一边的桌沿,所以说球并不会就此停下来。然后,球会重新滚回到最初的位置,如此循环往复。如图所示,简单概括来说就是,把球放在完全光滑的桌面边沿,它会无休止地运动(前提是桌面没有摩擦力和空气阻力的存在)。
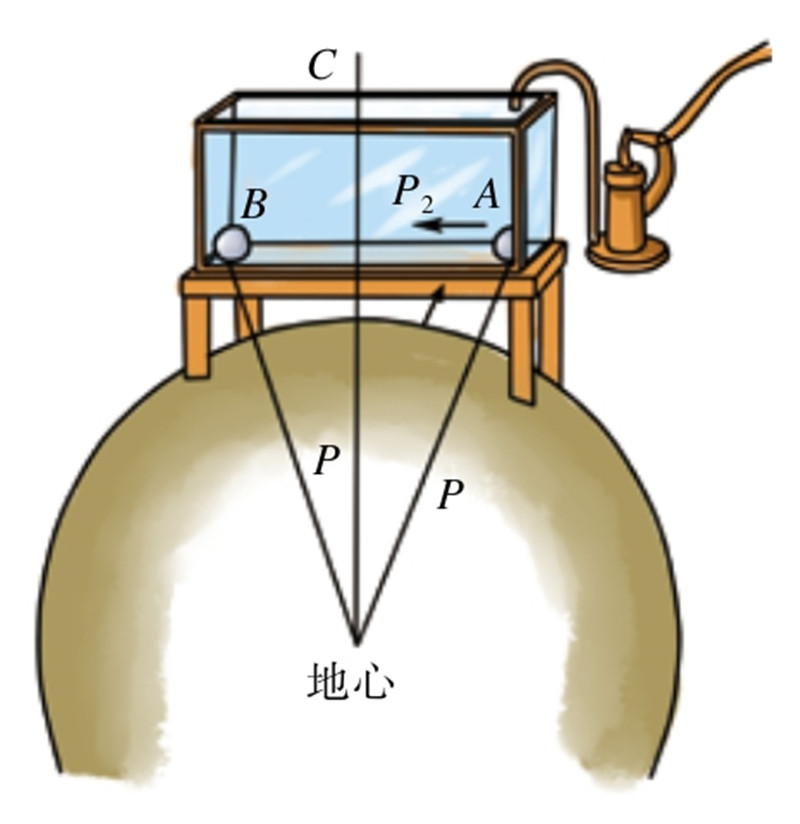
一个美国人想通过上面这个原理发明出永动的东西来。如图所示,是根据上述原理设计出的永动机图解,理论上来说他的方案是完全正确,而且永动也是完全可行的,前提是发明出的这个东西能够摆脱摩擦力的影响。
我们认真思考一下,似乎有一个更简单的方法也可以实现永动,即借助于绳上晃动的重物:这个重物在不考虑支点上面的摩擦力及空气阻力的情况下,就能够永久地晃动。
下面我们再来看一下一个具有借鉴意义的反方观点。提出这一观点的是一名读者。他解释说,我们认为在球体表面太阳光线是聚焦的,这是从几何角度来看的;而从物理角度来说,我们认为这些光线是平行的。同理,在我们的实验中,从几何角度来看,两条同时穿过地球相距为1米的铅垂线是穿过了地心,但是从物理上来看是平行的。而从物理上来说,吸引球从桌沿向桌中心运动的力是等于零的;所以不可能观察到任何滚动。即他认为我们的论述是混淆了几何和物理这两个角度的问题。
反方的观点是不正确的。下面我们做一下计算:假如桌长1米,推动球体从桌沿滚动起来的力的大小约为球体重量的1/10 000 000;两条铅垂线之间相距1米穿过地球,它们之间构成了一个角度,这个角度与指向那些点的太阳光线角的比值是23 000:1。完全不考虑阻力的情况下(即在实验室条件下),无论物体的质量有多大,要推动该物体运动也只需要付出一个非常小的力就能够做到。何况出现在上面的情况中的那个力并不小:它类似于一个能引发海潮的力;即使是考虑阻力(即现实情况下),很明显地,后一个力也能够发挥出它的作用。
小贴士
巴黎天文台曾经在支点摩擦力最小的情况下,做过一个真空摆锤实验:摆锤晃动了30个小时。人们感兴趣的是,挂在伊萨基耶夫教堂上98米高的摆锤是如何慢慢停下来的。最初12米的摆幅经过3小时后会减小为原来的1/10。开始观察6小时后,摆幅又会缩减为6厘米,开始观察12小时后,肉眼基本就看不出摆幅了。
