【题】一根线轴系在活动的带子上,它落下后还会自己再弹上来,这是一种游戏,叫作“悠悠”。这种游戏并不是什么新鲜事儿,它早在《荷马史诗》中就已出现,古代英雄和智者就曾经玩过。
“悠悠”这个游戏,从力学的角度分析,也只不过是众所周知的“麦克斯韦”摆轮(见图12)的变体。在麦克斯韦摆轮实验中,当落下一个小飞轮时,它会将拴在其上的轴线带动着一起运转。一个很大的旋转力逐渐地形成,促使伸展到底端的轴线继续旋转,进而将飞轮重新带动起来,继续向上运动。飞轮在上升过程中,之所以会旋转得越来越慢,直至最后停止运动,再重新旋转下落,就是因为动能逐渐转化成了势能。最初的能量以热的形式在摩擦中消耗掉,此过程中,飞轮可以重复多次起落。
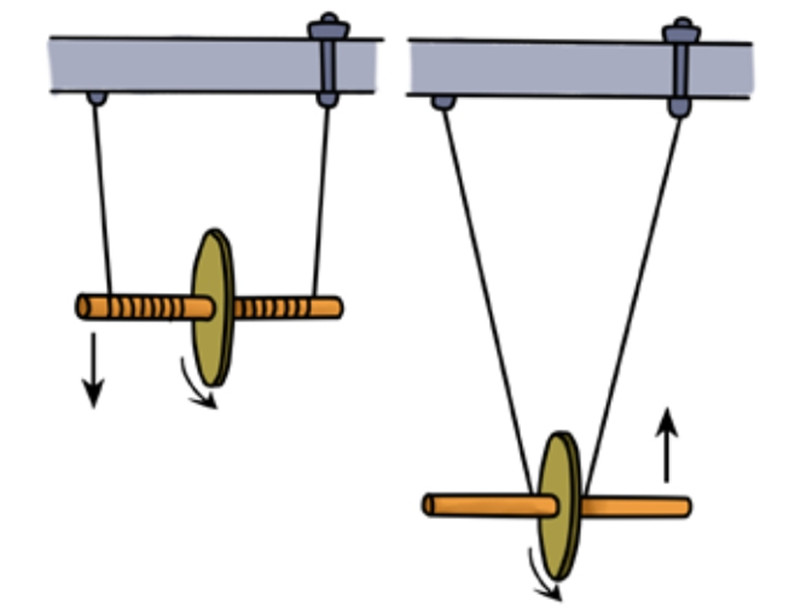
上面我们将“麦克斯韦”的实验描述了一下,进而提出下列问题。
如图所示,在弹簧秤上将麦克斯韦摆轮的轴线固定好,弹簧秤上面的指示针在小飞轮上下舞蹈时,会保持在原来位置,还是会发生变化?

【解】当飞轮向下运动时,弹簧秤的指针是不会上升的,因为轴线受到的并不是飞轮全部重量的拉力。所以,在这个实验过程中,指示针在飞轮落下之前,都会处于一个微微翘起的状态。虽然计算出这样的结果让我们感到意外,但是这个结果由实验证明却是正确的。

指针会在飞轮上升直至最高点(此时飞轮就像瞬间静止)的过程中,一直保持着这个状态。以此类推,指针只有在飞轮处于运动路线最低点的时候,指针的刻度才会显示减少,而到下一刻则又会恢复到原先的状态。
下面我们再论证一下上述结论。我们假设飞轮的质量用m表示,自由落体加速度用g表示,飞轮落下的高度用h表示,平移运动的速度用v表示,旋转运动的角速度用ω表示,飞轮的惯性力矩用k表示。mgh表示势能转化为平移运动的动能mv2/2和旋转运动的动能kω2/2。因为飞轮向下的运动就是一个匀加速运动,而这个加速度与自由落体加速度相比要小一些。根据能量守恒定律,我们就可以列出下面这个算式:
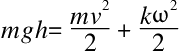
同时,我们可以用qmv2来代替等式的右侧部分,因为飞轮的旋转运动能量是它平移运动能量的几分之一。而这里的q只受飞轮的惯性力矩k决定,它是一个抽象数(或者是一个单位)。所以q在飞行过程中是不会改变的。那么就有
mgh=qmv2
由此可见
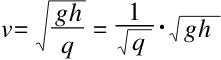
自由落体的公式为
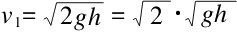
我们将上面两个公式对比一下就可以看到,飞轮的下落速度(在每个点都是相等的)即是自由落体速度的几分之一:
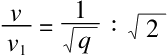
得出
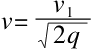
另外,v1=gt(自由落体的速度v1与它的持续时间t之间是存在这种关系的),所以
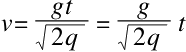
通过上述公式我们可以得出,飞轮在以匀加速度向下落的时候,加速度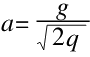
。又因为q>1,所以a<g。
依次类推,我们同样可得出,飞轮是通过匀减速的运动来完成上升的,无论是大小还是方向,这个加速度同样是a。
由于飞轮向下运动就是受到了小于它重量的力的作用的影响,所以很显然,它就受到某个向上的力f的牵引:f=mg-ma,即f等于飞轮重量mg和牵引飞轮运动的力ma之间的差,这也是轴线的拉力。只要确定了加速度的大小,我们也就可以知道在飞轮上升和下落运动中飞轮轴线所受到的拉力了。
由此可见,弹簧秤的指示针在飞轮下落时应该高于飞轮的重量刻度。
当飞轮向上运动的时候,我们就用得出的飞轮下降的公式来表示轴线的拉力:
f=mg-ma
所以说,弹簧秤的指示针不会受到飞轮上升或者下降的影响,依然保持不变。
在飞轮运动到最高点时,这个等式f=mg-ma依然是成立的:指针的状态不会受到飞轮自上而下运动时的影响。
那么相反,在飞轮运动到最低点时,弹簧秤指示针的刻度要比整个飞轮重量所称出的刻度低。当时飞轮悬在紧绷的绳上,附着点传送其全部重量的同时,还传送飞轮轴运动的离心力(沿着小半径的弧形传送)。当飞轮运动到最低点时,飞轮将绳子解开到末端后,从一个方向转入另一个方向,此时绳子猛然一拽,出现一股拉力,指示数值就会瞬间下降。
