首先,让我们来看一条放之古今皆准的原则:没有交配,物种就无从诞生。接受这条原则,并不意味着对恋爱关系、灵性修养、性取向多样性或是寻找幸福的美好愿望的排斥。但在现实中,为了避免绝迹,以下几个目标是每个物种都必须跨过的门槛:

1.活到能够交配的岁数。
2.吸引伴侣,生育后代。
3.把这些后代抚养到能够生育的年龄。
若要更好地理解这些目的,我们不妨将生育作为整个择偶竞赛的目的。如果你的孩子成功找到了配偶并生育了后代,你就更有理由相信你的家族以及整个人类存活下来的可能性会更大。在人口过剩造成的问题大于灭绝之灾的今天,这样的理念听起来或许有些杞人忧天,但是在很长的一段时间里,人们都无法保证自己的孩子成活到能够生育的年龄,因为在19世纪中期之前的几千年中,满足人类的基本温饱是一件异常困难的任务。
20世纪50年代颇具影响力的心理学家马斯洛提出了一套有关动机的理论,被称为马斯洛需求层次理论。依照这个框架,我们可以对长久以来影响人类择偶方式的力量有一个很好的了解。马斯洛的需求层次理论指出,人类会依从低到高的顺序来满足自我需求,最低层的需求包括如食物和水在内的生理需要,依次往上排列,还有安全需要、社会需要、尊重需要和自我实现,排列在最高位置的自我实现是一种心理需求,也就是指个人将潜力发挥到最大程度的状态。几千年来,人类努力寻找居所、洁净的水源、可长期依靠的食物供给,还要在各种势力的斗争或捕食者的夹缝中寻求安全庇护。由于生存的基本条件难以达成,人类便将这些基本需求当成了婚姻大计的坐标。
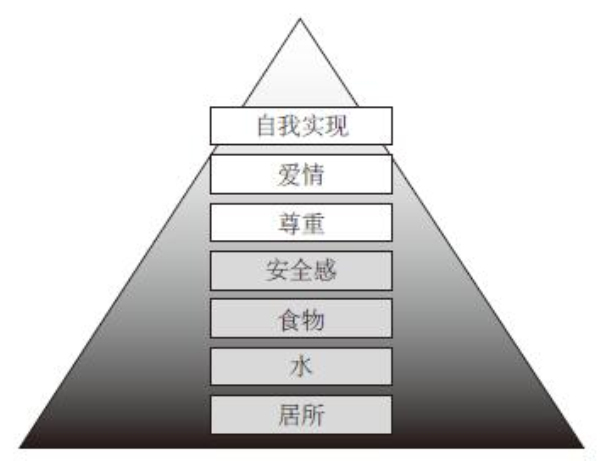
图3–1 马斯洛的需求层次
为了生存
由伦敦格雷沙姆学院的罗德里克·弗拉德以及芝加哥大学的罗伯特·福格尔带队,一批卓越的研究人员花了数十年的时间进行了一项研究,将婚姻出现后前4850年的背景清晰地呈现在了我们的面前。在19世纪中期之前,人类的平均寿命不足40岁,而只有1/3的孩子能活到自己15岁生日那一天。造成年人类平均寿命较短的原因包括不洁饮用水、食物匮乏、传染病以及大规模战争等。
19世纪早期,在西欧国家中,大约有10%的人不到15岁就因饥饿而死。此外,更有20%的家庭长期处于营养不良的状态,而在这些家庭出生的孩子即便存活下来,也很有可能会患上智力残障和身体发育不良等疾病。假设你的家人有30%被饿死的概率,你的孩子也有可能长期罹患发育不良造成的疾病,那么你在择偶竞赛中的需求就是要找到一个能够最大限度地提升家庭存活率的对象。
为了解释保命这项任务有多么艰巨,让我们来看一看人们是如何满足对食物的需求的。在19世纪初,每人每天平均能够摄取到的能量为2118卡路里,而那些久坐不动的人只需要1843卡路里就可以存活。因此,对一般人来说,每人都有275卡路里的额外能量可以用于工作或休闲娱乐。但是,为了完成满足基本需求所要完成的工作,一般人很快就会将这少量的能量盈余消耗掉。如图3–2所示,我们可以看到为满足基本需求所必须进行的工作所消耗的卡路里量,比如,种田30分钟需要消耗195卡路里,而砍柴30分钟则需要消耗258卡路里。放在当今的背景下来看,如果每人每天只有275卡路里的盈余,那么只能上一个小时的瑜伽课,我们就得终日躺在床上维持生命了。
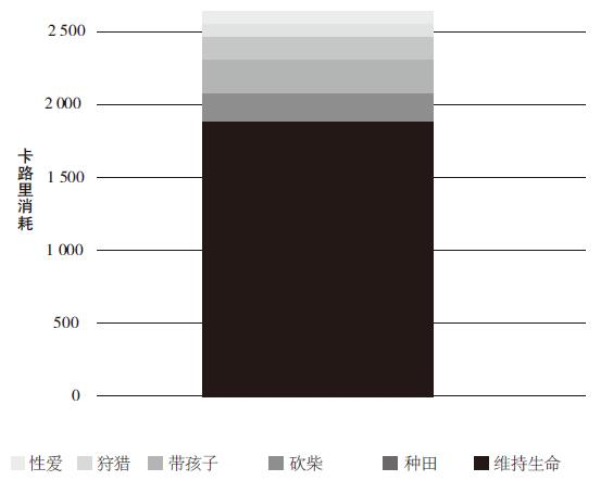
图3–2 各项活动所需的卡路里
在19世纪中期之前,人们所摄取的能量很少,想要获取额外的能量,他们就不得不消耗更多的能量。这便是当时的人们需要面对的难题。在遗传和体力上能够有效利用有限资源的人自然受到大家的追捧,除此之外,人们也希望通过狩猎、采集或是社交找到高于平均值资源的对象。可是,即便是在几千年前,优质的对象也是非常难寻的。
寻找优质伴侣
寻找和吸引优质的对象,可以增加一个家庭得以生存下去的概率。然而,由于狩猎采集或小型农耕组群的规模很小,可供选择的对象也很有限。有的组群,甚至只有25~50人。在任何指定的时间段内,组群中能够作为伴侣人选的人更是少得可怜,这就好像是在一所小型的乡村学校里寻找毕业舞会的舞伴一样。让我们尽可能地把条件放宽,试想在一群年轻人中,共有50名单身汉。我们来看一看,如果有人对理想伴侣的特质提出了三个适中的要求,会出现什么情况。
第一个愿望是,要求对方的身高属于中等以上,也就是说要高于1.72米。在工业化之前的社会,由于营养匮乏和疾病等健康风险与人的健康和寿命紧密相关,所以身高是身体健康的一个非常可靠的指标。第二个愿望是,要求对方有能力承受的工作量高于一天9个小时的平均值。这个愿望很明智,因为工作可以提供一家人生存所需要的一部分能量。高于1.72米的身高要求,将50名可选伴侣中80%的人淘汰出局,而能够获取9个小时的工作量所需能量的人也仅占10%,也就是说,在剩下的10个人选中,只有一人符合标准。那些希望伴侣的头发是咖啡色而不是金色,或是身着时髦皮草背心而不是皮革背心的愿望,大可以省省了,仅仅要找一个能够干一整天活的伴侣,就已经够困难的了。
表3–1

好戏还在后头呢。每个人都想找一个能够提高家庭生存概率的伴侣,这也为求偶之战创造了条件。现在的一些电视节目要么是拿泽西海滩边发生的恋情闹剧大做文章,要么就是记录一群单身汉为了博得一位单身美女的芳心而你争我斗,为了重现求偶竞争的状况,我们可以参照一下这些电视节目中所呈现的情景。制作人故意将一小组躁动的单身男女安排在狭小封闭的空间里,运用这种手段巧妙地制造出夺人眼球的节目效果。
两性之间的吸引力造成了情感激烈的利益冲突,而这些制作人则坐等由冲突而产生的人际矛盾的出现。在这些真人秀节目的开头,我们能看到,随着一个族群之中最优秀的男性与女性的出现,一场竞争也在酝酿之中。每个人都已做好准备,想要从候选人之中吸引到最佳的伴侣。嫉妒滋生出激烈的竞争,闺密反目成仇变为劲敌,最终,整个群体仿佛都悬在了分崩离析的边缘。
当人们在小规模团体中生存时,由有限资源造成的空间资源稀缺,加之为生存起见而不得不紧密团结在一起的需求,注定催生人们在求偶竞赛中,当个人利益遭到削弱时所产生的争执和钩心斗角。但是,与电影《泽西海岸》或《老大哥》中呈现的纷扰不同,在现实生活中,我们的祖先在感情纠葛上花费的精力,削弱了他们本可以用来收集生存所必需的资源的精力。
在一场没有裁判的求偶竞赛中,如果我们放手让自私、嫉妒以及仇恨之情任意滋长,那么最终人人都有可能蒙受损失。因此,明智之人提议,要通过设置规矩来让这场找寻优质伴侣的竞争变得井然有序。也许是为了缓解人与人之间的摩擦所造成的纷扰,5000年前,婚姻这项制度便问世了。
在《婚姻的历史》一书中,孔茨教授告诉我们,婚姻制度已经存在于世5000年,在其中的大部分时间里,我们的社会因婚姻制度而变得更加和谐。当时,个人的生存依靠小规模团队天衣无缝的配合,而争取优质对象的竞争也异常激烈,在这种情况下,婚姻为社会带来的和谐性显得尤为重要。按照当时的婚姻流程,年轻人的双亲需要扮演相当于代理人或中介的角色,订立与婚姻的相关“合同”。这些合同规定,女儿的终身要以男方家的地产、牲畜或资金作为交换;每个家庭都有一个最为重要的目标,那就是希望创造能够增加家庭资产或提升家庭地位的条件。这不但可以提高孙辈获得丰富资源的概率,也让他们有更大的可能找到出身名门的优质伴侣。
抚养健康的子孙
如果某人在17岁时产下了第一个孩子,并想要活着看到自己的孩子结婚生子,那么在这个社会中,寿命达到35岁的人所占的比率便是求偶成功率的一个重要指标。在18世纪初的法国,孩子成长到17岁之前就去世的概率为27%,而活不过35岁的概率则为45%。
切记,传递基因、抚养子嗣、确保你的孩子也能够繁衍后代,这些一直都是求偶的最终目的。由于你的孩子有可能活不到能够生育的年龄,所以选择一个能够增加孩子生存概率的配偶自然也就成了大事。毋庸赘述,你需要寻找一位最有能力帮你实现这个目标的人选。如果你周围经常有人因疾病而死,那么你当然想要选择一位看上去很健康的伴侣。同理,如果你常常受到饥饿的折磨,甚至威胁到了你及你孩子的生命,那么选择能带来最多食物资源的配偶自然也就合情合理了。所以说,体魄健康且能够最大限度地提升你和你后代生存概率的人,自然也就是最理想的配偶人选了。
研究人员会用到“繁育力”这个词,来形容候选配偶在求偶成功率及其后代求偶成功率方面的心理和生理的健康条件。虽然许多人的孩子都活不到能够生育的年龄,但人们最主要的目标仍是选择适合繁育的配偶,因为这样的配偶更有能力提供如食物和蛋白质一类的资源。同时,适合繁育的配偶也会传播所谓“优质的基因”(比如强壮的免疫系统和体能),这些也是提高后代生存概率的条件。通过日常观察,我们不难发现,从基因上来说,个头高的双亲比较容易生出高个子的孩子,相貌出众的双亲更容易生出长相好看的孩子,而情绪稳定的双亲则比较容易生出沉稳的孩子。
从体貌特征来看,外貌出众的配偶具有更加适合繁育的条件。同时,心理特质也与配偶候选人的繁育力有所关联。关于择偶时大家所偏重的个性、能力或价值的研究和理论有成百上千种,举例来说,相对于男人而言,女人在挑选长期伴侣的时候会更加看重对方是否和善。虽然男女都希望自己的伴侣性格好,但承担着怀孕、生产以及抚养孩子重任的女性,更加希望选择会对自己和孩子的福祉负责且温柔和善的配偶。类似的研究结果还有很多,比如说,人们偏爱能力强的配偶,因为这些人在社会等级的竞争中更有可能占领有利地位;人们还偏爱有智慧的配偶,因为他们更有可能有效地解决与生存相关的问题;另外,人们也偏爱认真负责的配偶,因为他们更有可能具备吃苦耐劳的职业道德。
以繁育力作为选择配偶的首要条件,这听起来的确不怎么浪漫,但是我们不难看出,在危险的求偶条件下,人们的确会逐渐对繁育力强的配偶产生偏爱。当死亡近在眼前时,以激情或心动作为结婚的首要因素看似是不符合常理的。这并不是说我们的祖先对浪漫的爱情无动于衷,而是说激情并非结婚最主要的原因。而17世纪初期一系列事件的发生,却为求偶竞赛的游戏规则带来了戏剧性的变化。
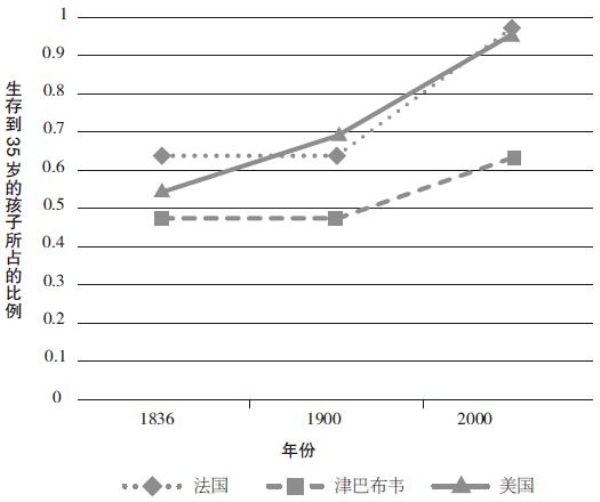
图3–3 17世纪初存活至35岁的孩子所占的比例
